Pótold az ábrán látható piramis hiányzó számait úgy, hogy minden téglán azon számok aritmetikai középértéke legyen, amelyek az adott téglánál sötétebb téglán találhatók!

Zsuzsa, Péter, Jakab és Anna golyóztak. A játék végén Zsuzsának néggyel kevesebb golyója volt, mint az összes golyó fele, Péternek hattal több volt, mint a golyók számának egyötöde, Jakabnak háromszor kevesebb volt, mint Zsuzsának, és Annának eggyel kevesebb golyója volt, mint Jakabnak. Melyik gyereknek volt a játék végén a legkevesebb és melyiknek a legtöbb golyója?

Az 5 cm oldalhosszúságú ABCDE szabályos ötszögben jelöljük meg az AC és BD szakaszok metszéspontját M betűvel. Számítsátok ki az AM szakasz hosszát és az AMB szög nagyságát!

Legalább hány tényezőt kell tartalmaznia az alábbi szorzatnak, hogy osztható legyen 100-zal?

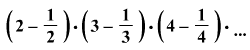
Rajzoltunk egy egyenlő oldalú háromszöget. Felosztottuk 4 egybevágó részre. Egyet közülük befestettünk, és a háromszög megmaradt részét megint felosztottuk 4 egybevágó részre. Rajzold le azt az ábrát, amelyet így kaptunk!

Szerencsés Szidónia szabadságolása idején 15-ször esett az eső, de sohasem egész nap. Ha délelőtt esett, délután napsütés volt. Ha ebéd után esett, azon a napon délelőtt volt napsütés. 9 délelőtt és 8 délután folyamán napsütés volt. Milyen hosszú volt Szerencsés Szidónia szabadsága?