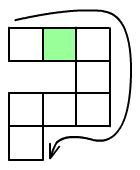
Egy kocka minden lapjára más-más 20-nál kisebb törzsszámot (prímszámot) írtunk úgy, hogy a szemben fekvő lapokon levő számok összege mindig ugyanannyi legyen. A kockát ráhelyeztük az ábrán látható játéktábla első mezejére a legkisebb számmal lefelé fordulva és a nyílnak megfelelően gurítottuk. Minden esetben, amikor a kocka lapja érintkezett a játéktáblával, az érintett mezőbe beírtuk az azt érintő lapon levő számot. Milyen számú lap érintette a kiszínezett mezőt, ha a beírt számok összege a lehető legnagyobb volt? (A játéktábla olyan négyzetekből áll, amelyek a kocka lapjaival egybevágóak.)

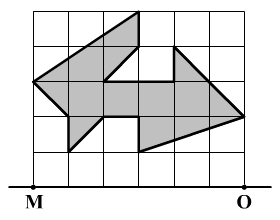
Az ábrán egy négyzetháló látható, amelyen a négyzetek oldala 1 cm hosszú. A négyzethálóban egy szürkére festett alakzat található. Libornak olyan egyenest kell szerkesztenie, amely párhuzamos az MO egyenessel és a szürke alakzatot két egyenlő területű részre osztja. Az MO egyenestől milyen távolságra rajzolja Libor ezt a párhuzamost?

A turisták egy háromnapos gyalogtúrát úgy terveztek meg, hogy minden nap megteszik az egész út egyharmadát. Ezt viszont csak az első napon tartották be. A második napon a megmaradt út egyharmadát, a harmadik napon pedig a fennmaradó rész egynegyedét tették meg. Az utolsó 24 km-en egy terepjáró vitte őket a célba. Milyen hosszúra tervezték az egész túrát és hány km-t tettek meg (gyalog) az első, második és a harmadik
napon?

Horák úr 3 évvel időseb mint felesége, és elsőszülött fiuk 4 évvel idősebb mint a másodszülött. Mind a négyen ugyanazon a napon ünneplik a születésnapjukat és most együtt 81 évesek. 5 évvel ezelőtt együtt 62 évesek voltak. Hány évesek most a szülők és hány éves a két fiú?

Zsuzsa leírt egy ötjegyű számot. Ha a szám végére odaír egy egyest, akkor olyan számot kap, ami háromszor nagyobb, mint az a szám, amit akkor kapott volna, ha az egyest az eredeti szám elé írja. Melyik ötjegyű számot írta le Zsuzsa?

Adott az ABCD téglalap. Az A ponton át felveszünk egy egyenest, amely a CD szakaszt olyan X pontban metszi, hogy a keletkezett alakzatok területeinek aránya S_AXD:S_ABCX = 1:2. Az X ponton át felveszünk egy egyenest, amely az AB szakaszt úgy metszi az Y pontban, hogy S_AXY:S_YBCX = 1:2. Most az Y ponton át ismét felveszünk egy egyenest, amely az XC szakaszt úgy metszi a Z pontban, hogy S_XYZ:S_YBCZ = 1:2. Számítsd ki a következő területek arányát: S_AXD:S_AXZY.