Egy tetszőleges több számjegyű szám számjegyeinek szorzata mindig kisebb, mint maga a szám. Ha kiszámítjuk az adott szám számjegyeinek szorzatát, azután a szorzat számjegyeinek szorzatát azután ismét az új szorzat számjegyeinek szorzatát, stb., akkor törvényszerűen valahány lépés után egy egyjegyű számhoz jutunk. Ezeknek a lépéseknek a számát az adott szám perzisztenciájának nevezzük. Pl. a 723 perzisztenciája 2, mivel 7.2.3 = 42 (1. lépés) és 4.2 = 8 (2. lépés).
• Keressük meg azt a legnagyobb páratlan számot, amelynek számjegyei kölcsönösen különböznek és perzisztenciája 1.
• Keressük meg azt a legnagyobb páros számot, amelynek kölcsönösen különböző nem nulla számjegyei vannak és perzisztenciája 1.
• Keressük meg a 3 perzisztenciájú legkisebb természetes számot.

Andris a kiránduláson elköltötte pénzének 2/3-át, a maradék 2/3-át pedig a tibeti gyerekek megsegítésére fordította. Az így megmaradt pénz 2/3-ából édesanyjának vett egy kis ajándékot. Az ezután megmaradt pénz 4/5-ét elvesztette, mert lyukas volt a zsebe. Mikor a megmaradt pénze felét kishúgának adta, éppen egy eurója maradt. Mekkora összeggel indult el Andris a kirándulásra?

Szilvia meséli: „Hárman vagyunk nővérek, én vagyok a legfiatalabb, Lívia három évvel idősebb, Edit pedig nyolccal. Édesanyánk szívesen hallja, hogy átlagéletkorunk (vele együtt) 21 év, mindemellett ő már 29 éves volt, amikor én születtem”. Hány évvel ezelőtt született Szilvia?

Gyuri leírt egy négyjegyű számot. Ezt a számot tízesekre, majd százasokra, majd ezresekre kerekítette és mindhárom eredményt leírta az eredeti szám alá. Ezután a négy számot összeadta és a helyes eredmény 5 443 lett. Milyen számot írt le Gyuri eredetileg?

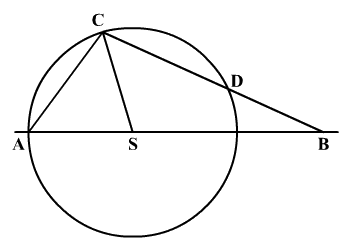
Laci rajzolt egy S középpontú kört és A, B, C, D pontokat, ahogyan azt az ábra mutatja. Megállapította, hogy az SC és BD szakaszok hossza megegyezik. Milyen az ASC és SCD szögek nagyságának aránya?

Keressük meg az összes olyan háromjegyű természetes számot, amelyek maradék nélkül oszthatók 6-tal és amelyekből bármely számjegy áthúzása után olyan kétjegyű természetes számot kapunk, amely ismét maradék nélkül osztható 6-tal.