Ha egy szám a 13 többszöröse, akkor „kissé szomorúnak”, ha 17-nek a többszöröse, akkor „kissé vidámnak” nevezzük. A természetes számsor 1-től 1 000 000-ig terjedő számai közül hányra áll fenn, hogy nem végződik se 0-ra se 5-re, „kissé szomorú” de ugyanakkor „kissé vidám” is?

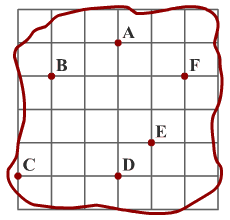
Meseország kormánya úgy döntött, hogy az ország területét hat megyére osztja fel. Ezért a hat legjelentősebb város (megyeszékhely) mindegyikének hatáskörébe rendelt egy területet (megyét), az alábbi szabály szerint: az ország bármely pontja abba a megyébe tartozik, amelynek megyeszékhelyéhez légvonalban legközelebb esik. Rajzoljátok át megfelelő mértékben Meseország térképét, és szerkesszétek meg benne a megyehatárokat! (Az A-F betűk a megyeszékhelyeket jelölik, a vastag vonal Meseország határa. A négyzetrács csak a térképen való eligazodást könnyíti, a megyehatárokat semmilyen módon nem befolyásolja!)

Délben a főtéren parkoló magyar, szlovák és osztrák rendszámú autók aránya a következő volt: magyar és szlovák 9:4, szlovák és osztrák 2:3. Egy óra alatt elment 11 magyar, 1 szlovák és 3 osztrák autó, de jött 5 magyar, 11 szlovák és 6 osztrák autó. Milyen a magyar, szlovák és az osztrák rendszámú autók aránya a parkolón délután egykor, ha délben a parkolón 12 osztrák autó állt?

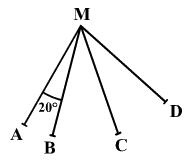
Az ábrán látható AM, BM, CM és DM szakaszok hossza azonos. Az általuk meghatározott szögek nagysága  20°, 20°, 50°, 50°, 70°  és α . Határozd meg az AB és CD egyenesek hajlásszögét! (Az ábra pontatlanul van megrajzolva, nem érdemes mérni.)

Egy 4x4-es sakktábla összes mezőjét négy színnel fessétek ki és írjátok rájuk a N, Y, Á, R betűket úgy, hogy minden oszlopban és sorban az összes szín és betű szerepeljen. Minden mező egyszínű legyen és pontosan egy betűt tartalmazzon. Mindegyik betűnek szerepelnie kell az összes színen és mindegyik színre rá kell írni az összes betűt. Keress egy megoldást!

Táblára írtunk néhány egymás után következő természetes számot. Közülük 12 szám az 5 többszöröse és 10 szám a 7 többszöröse.
a) Hány természetes számot írtunk a táblára?
b) Keress egy olyan számsort, amely megfelel a fent leírt feltételeknek!