Évi egy olyan hatszöget szerkesztett, amelynek oldalhosszai cm-ben kifejezve egész számok. Megfigyelte, hogy a hatszögnek csak merőleges oldalpárjai vannak. Hogyan nézhetett ki Évi hatszöge, ha tudjuk, hogy kerülete 16 cm és területe 12 cm² ? Mindkét megoldást szerkeszd meg!

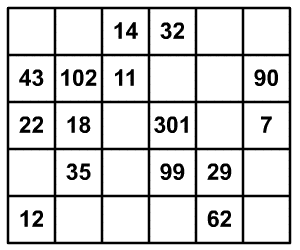
Vágd szét a téglalap alakú négyzetrácsot (lásd az ábrát) a lehető legkevesebb egybevágó részre úgy, hogy mindegyik részben a számok hárommal osztva különböző maradékot adjanak! Vigyázz, vágni csak a háló vonalai mentén szabad!

Határozd meg azoknak a törteknek a számát, melyeknek értéke a három többszöröse és számlálójuk valamint nevezőjük háromjegyű természetes szám!

Egyszer egy gazda búzát vitt a malomba. Az egyik zsákja lyukas volt, így a magok az útra szóródtak. Észre vette ezt egy zöld, piros és egy kék madár. Elsőként a zöld madár szállt le és minden negyedik szemet felcsipegetett a földről. Utána a piros madár minden ötödiket és legvégén a kék madár minden harmadik szemet csipegette fel. Hány búzaszemet veszített a gazda, ha a madarak összesen 79 magot ettek meg?

„Hullámosnak” nevezzük azt a különböző számjegyekből álló három-, vagy többjegyű számot, amelyben nincsenek olyan egymás után következő a, b, c számjegyek, amelyekre fennállnának az a<b<c vagy a>b>c egyenlőtlenségek. Írd fel:
a)   a legnagyobb 3-mal nem osztható „hullámos” számot!
b)   a legnagyobb 150-nel osztható „hullámos” számot!

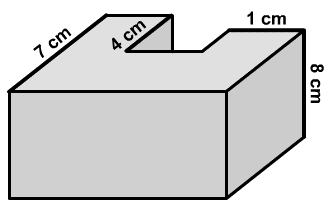
Három téglatest összeragasztásával egy nyolcoldalú egyenes hasábot kaptunk (lásd az ábrát). Számítsd ki a hasáb térfogatát és felszínét, ha ismered a kijelölt élek hosszát és tudod, hogy mindegyik oldallapnak pontosan egy egybevágó párja van!