|
|
|
Matematikai Olimpia, 7. évf., 2004/05, I. ford. feladatai
-
Hosszú,
Széles és Élesszemű mérték a magasságukat. Megállapították, hogy Hosszú
kétszer olyan magas, mint Széles. Élesszeműnek a magassága kétharmada Hosszú
magasságának, de 44 cm-rel magassabb, mint Széles. Határozzátok meg, hogy
milyen magas Hosszú, Széles és Élesszemű.
-
Adva van egy hárommal osztható
ötszámjegyű szám. Ha ezen számból kihagyjuk a páratlan helyen álló
számjegyeket, akkor 67-szer kisebb kétszámjegyű számot kapunk azon számnál,
amelyet az eredetiből a páros helyen álló számjegyek kihagyásával kapunk.
Határozzátok meg ezt az ötszámjegyű számot.
-
Számországban csak természetes számok élnek. A férfiak és
fiúk páros, a nők és leányok páratlan számok. A házaspároknak
gyermekeik születnek rögtön a házasság után, mégpedig az összes olyan
számok, amelyek maradék nélkül osztják a szülők
szorzatát.
a)
Melyik udvarlót a 2, 16, 28 és 46-os számok közül válassza ki
a Kilenceske hölgy, ha minél több különböző gyermeket
akar?
b) Melyik udvarlót a 2, 16, 28 és 46-os számok közül válassza ki a
Kilenceske hölgy, ha ugyanannyi fiút akar mint leányt, de egyetlen egyenlő
gyermeket se nem akar?
-
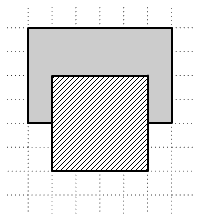
Kamilka a
négyzethálóba téglalapokat rajzolt (a négyzet a téglalap speciális esete).
Közben érdekes téglalapkettőst talált: egy 6 cm és 4 cm
oldalhosszúságú téglalapot és egy 4 cm oldalhosszúságú négyzetet. A
hálóba először a téglalapot rajzolta be és utána a négyzetet (ábra).
Meglepetéssel vette észre, hogy a téglalap nem lefedett részének
a területe egyenlő a négyzet területével és a téglalap nem lefedett
részének kerülete egyenlő a négyzet kerületével.
A
következő téglalapokból válaszd ki az összes téglalapkettőst, amelyek mindkét
Kamilka által felfedezett tulajdonsággal rendelkeznek:
3 cm × 9 cm, 4 cm × 9 cm,
4 cm × 6 cm és
5 cm × 7 cm.
-
Rágcsálóegérke sajttéglát talált. Az első nap a
sajt  -át, második nap a
maradék -át, második nap a
maradék  -ét,
harmadig nap a maradék -ét,
harmadig nap a maradék  -át és negyedig nap a maradék -át és negyedig nap a maradék 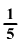 -ét ette meg. A sajtból egy
150 cm2 felszínű kocka maradt. Milyen volt az eredeti sajttégla
köbtartalma? -ét ette meg. A sajtból egy
150 cm2 felszínű kocka maradt. Milyen volt az eredeti sajttégla
köbtartalma?
-
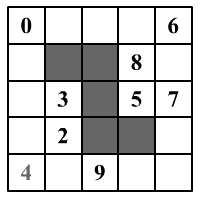
Az
archeológusok egy papyrus-t ástak ki, amelyen egy érdekes tábla Z alakú
kivágassal volt (ábra). Feltételezik, hogy az egyik ú.n.
Összeadók indián törzs talizmánja lehetett. Ezen törzs
mindegyik talizmánja a következő tulajdonsággal rendelkezik: ha tetszésszerint
beköröztök benne öt számot úgy, hogy minden oszlopban és sorban pontosan egy
szám van bekörözve és összeadjátok ezen számokat, mindig ugyanazt az összeget
kapjátok. Próbáljátok megrestaurálni az ábrán látható talizmánt, tehát
írjátok be a hiányzó számokat.
|
