A csillagok helyébe írj számjegyeket úgy, hogy az egyik példa eredménye 23-szor nagyobb legyen a másik példa eredményénél.

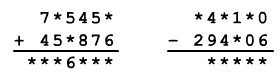
Az udvari matematikust múlt havi keresetének nagyságáról faggatták. Ő így válaszolt: "Ha a számhoz - amely a keresetemet koronákban kifejezi - hozzáadjuk az összes olyan számot, melyet az eredeti szám számjegyeinek a felcserélésével képeztünk, 4218-at kapunk. Keresetemet a lehető legkevesebb egy-, tíz-, illetve százkoronással fizették ki." Hány "darab" fizetőeszközt kapott a matematikus? Legalább és legfeljebb hány koronát kereshetett?

Egy téglalapnak és egy háromszögnek ugyanakkora a kerülete. Mindkét alakzat oldalainak mérőszáma egy-egy kétjegyű természetes szám. Az oldalakhoz írt számok "lepotyogtak" egy kupacba, és a következő számcsoport keletkezett: 0 1 1 1 1 1 2 3 4 4 4 5 6 6. Mekkorák lehettek az alakzatok oldalainak eredeti mérőszámai? Keress legalább három megoldást!

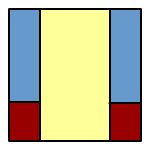
Palkó egy téglatest lapjait három szín valamelyikével színezte ki - a szemközti oldallapok ugyanolyan színűek, miközben mindhárom színt felhasználta. Utána a téglatestet egy papírlapon az élei mentén forgatta. Így az alábbi ábrán látható négyzet keletkezett. Határozd meg a téglatest méreteit, ha tudod, hogy a négyzet területe 36 cm². (A feladatnak két megoldása van.)

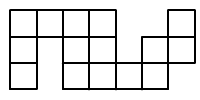
A téglalapból kinyírtuk területének 11/16-od részét, és az ábrán látható alakzatot kaptuk. Milyenek lehettek az eredeti téglalap méretei?

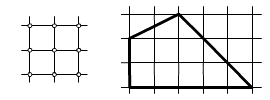
Adott egy négyzetrács 9 pontja (ábra). Határozd meg az összes olyan különböző, nem egybevágó háromszöget, melynek csúcsai rácspontok, majd fedd le ezekkel a háromszögekkel az ábrán látható négyszöget. (A háromszögek nem fedhetik egymást.)