Lenka egy érdekes számsorozatra bukkant a könyvében. A sorozat minden tagja megegyezik az őt megelőző két tag szorzatának számjegyösszegével. A kislány elárulta, hogy ebben a sorozatban az első helyen a nyolcas szám áll, a harmadik helyen egyjegyű szám áll, a negyedik helyen pedig a 2-es szám van. Milyen szám állhat ebben a sorozatban a hatodik helyen?

Az ABC háromszög egyenlő szárú. Az AC és BC szárai 36°-os szárszöget zárnak be egymással. A CAB szög tengelye a BC oldalt egy D pontban metszi. A CD szakasz hossza 8 cm. Milyen hosszú az AB oldal?

A cukrászdában 2 dl narancslé ára 12 Sk, 2 dl almléé pedig 8 Sk. Külön kérésre almalé-narancslé keveréket is készítenek. Ebben a keverékben az almalé és a narancslé aránya olyan, hogy a két összetevő árban megegyezik. Mennyibe kerül 2 dl ilyen keverék? (A keverék elkészítéséért nem számítanak fel semmit.)

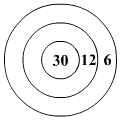
Tell Vili az ábrán látható céltáblára lőtt:
- húsznál többször nem lőtt;
- minden nyíl eltalálta a céltáblát, s egy lövéssel átlagban 17 pontot szerzett.
Lefeljebb hány pontot szerezhetett Vili?

Az ABCD téglalap egyik oldala kétszer rövidebb a KLMN rombusz egyik átlójánál. A KLMN rombusz egyik oldala ugyanolyan hosszú, mint az ABCD téglalap egyik átlója. A KLMN rombusz területe 36 cm². Mennyi az ABCD téglalap területe?

Az öreg kalóz hátrahagyta a sziget térképét, a kincsekhez vezető út leírásával együtt: "A kereszttel megjelölt helytől az összes lépésszámnak a felét tedd meg keletre, utána 12 lépést menj észak felé. Majd fordulj ismét keletnek és tedd meg a kincsekig hiányzó lépések harmadát. Azután fordulj északkeletnek és tedd meg a hiányzó lépésszám felét. Ha még 189 lépést megteszel északnak és végül 57 lépést északnyugatnak, eljutsz az elásott kincsekhez." Hány lépés megtételére van szükség a kereszttől a kincsekig?