|
|
|
Matematikai Olimpia, 7. évf., 2003/04, I. ford. feladatai
-
Hófehérke a múlt héten két
doboz csokoládédrazsét vásárolt. A két egyforma doboz tartalmát
igazságosan úgy osztotta el a hét törpe között, hogy
mindegyiknek 5 szem jutott. Azokat a szemeket, amelyeket már nem
tudott igazságosan kiosztani, megette. Ezen a héten Hófehérke ismét
vásárolt csokoládédrazsét, mégpedig 3 dobozzal, ugyanabból a
fajtából, mint a múlt héten. Ismét elosztotta a drazsét a hét törpe
között, a fennmaradó szemeket ismét megette. Most azonban kevesebb
szem jutott neki, mint a múlt héten. Hány csokoládédrazsé
lehetett egy dobozban?
-
Édesanya fánkot sütött.
Illata odacsalogatta a gyerekeket. Palkó eggyel kevesebb fánkot vett
el, mint az összes fánk egyharmada volt, Szerénke a megmaradt fánk
egyharmadánál eggyel kevesebbet, végül Mariska a maradék fánk
egyharmadánál eggyel kevesebbet vett el. A tányéron 11 fánk
maradt. Hány fánkot sütött édesanya összesen?
-
Két egyforma papírháromszögem
van. Ezekből össze tudok rakni (átfedés nélkül) egy téglalapot,
amelynek kerülete 21 cm, de egy ferdeszögű paralelogrammát
is, amelynek kerülete 24 cm, sőt egy háromszöget is, amelynek
kerülete 27 cm. Mekkorák a két papírháromszög méretei?
-
Az 1, 2, 3, ... 9 számokat
írjátok be az 1. ábrán látható négyzetekbe úgy, hogy minden
"hármasablakban" a számok összege egyforma és a lehető
legnagyobb legyen!
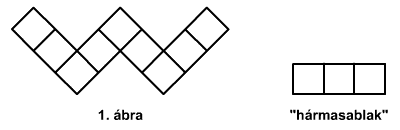
-
Egy ismeretlen vandál kitépett
a könyvből egy lapot. A megmaradt oldalakon a számozás számainak
összege 11011. Hány lapja volt eredetileg a könyvnek és milyen számozás
volt a kitépett lap oldalain? (A könyvben minden oldal meg volt számozva
és a számozás 1-gyel kezdődött.)
-
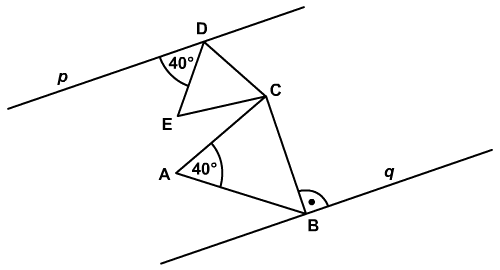
Az ábrán két párhuzamos p és q egyenes látható, közöttük
fekszik az ABC háromszög és a CDE háromszög. Érvényes:
• D
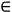 p és B
p és B
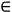 q, q,
• az ABC háromszög
egyenlő szárú,
• a CDE háromszög
egyenlő oldalú.
Számítsuk ki az ECA szög nagyságát!
|
