|
|
|
Matematikai Olimpia, 7. évf., 2001/02, I. ford. feladatai
-
Janka sálat kötött testvérének,
Lukácsnak. Lukácsnak a sál egyáltalán nem tetszett, ezért minden
este titokban Janka aznap megkötött sorainak a negyedét kifejtette.
Janka hétfőn kezdte kötni a sálat. Kedden 24 sorral többet kötött
mint hétfőn. Szerdán kétszer annyit kötött mint hétfőn. Csütörtökön
már csak 36 sort kötött és a kész, 180-soros sálat odaadta Lukácsnak.
Hány sort kötött Janka kedden? Összesen hány sort fejtett ki Lukács?
-
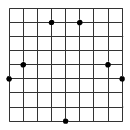
Az ábrán látható négyzethálón
ki van jelölve két négyzet összes csúcsa. Határozd meg a két négyzet
közös részének a területét.
-
Majonak össze kellett
szoroznia két tizedes számot. A tizedes vesszőket összetévesztette
a szorzás jelével (ponttal) és így négy egész számot szorzott
össze. Hiba nélkül számolt, eredményül 15228-at kapott. A helyes
eredménynek azonban 589,17-nek kellene lennie. Milyen számokat
kellett eredetileg összeszoroznia?
-
A táborban a vezetők szétosztották
a gyerekeket 5-ösével csapatokba, de az utolsó csapat nem volt
teljes. Ezért az új játéknál már 8-asával próbálták meg szétosztani
őket, de igy sem "jött ki". A második játéknál így 4
csapattal kevesebb csapat versenyzett mint az elsőnél. A nem teljes
csapatokban mindig páros számú gyerek volt. Mennyi gyerek lehetett
a táborban?
-
Jelöld meg a kocka csúcsait
egész számokkal 1-től 8-ig úgy, hogy a kocka minden egyes lapjára
a laphoz tartozó számok összege:
a) prímszám,
b) különböző prímszám legyen.
-
Az öreg farmer úgy döntött,
hogy az összes vagyonát - egy csorda bárányt - szétosztja
a gyerekei között. Először a csordát két részre osztotta 1:3 arányban.
A kisebb részt odaadta elsőszülött fiának, a nagyobb részt ismét
szétosztotta 1:3 arányban. Az új részekből a kisebbet odaadta másodszülött
fiának, a nagyobb részt ismét szétosztotta 1:3 arányban. Ezt
addig folytatta így, míg nem kapta meg az összes fiú a részét,
majd a megmaradó részt odaadta egyetlen lányának. Határozd meg,
mennyi báránya volt a farmernak, ha tudod, hogy a középső fia 156
bárányt kapott. Melyik gyereke kapta a legtöbb bárányt?
|
