|
|
|
Matematikai Olimpia, 5. évf., 2006/07, I. ford. feladatai
-
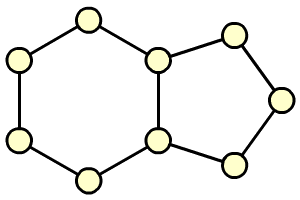
Az ábrán olyan ötszög és
hatszög látható, melyeknek egy közös oldaluk van. Írd a körökbe az 1,2, 3,
4, 5, 6, 7, 8 és 9 számokat úgy, hogy a hatszögben és az ötszögben is a
számok összege egyaránt 24 legyen! Minden számot pontosan egyszer
használhatsz fel. Elég, ha egy megoldást találsz.
-
A Keresztül-kasul
kerékpárversenyen 6-tagú csapatok vettek részt egész Európából. Az első 10
szakaszt még mindannyian teljesítették, de a 11. szakasznál egy tömeges
bukás után 17 kerékpáros visszalépett. A többi szakaszon fokozatosan, mindig
3-mal csökkent a visszalépők száma. Az utolsó, 15. szakasz végén 53
versenyző ért célba. Hány csapat vett részt a versenyen?
-
Tomi „Lajos” nevű idomított
bolhája az óra számlapján a 12-es szám melletti ponton állt. A
következőképpen játszottak: Tomi dobott a játékkockával, és a bolha a dobás
értékének megfelelő számú pontot ugrott. Az első dobás után az óramutató
járásával megegyező irányban ugrált, a második után ezzel ellenkező irányban
és a harmadik után újra az óramutató járásával megegyező irányban. Tudjuk,
hogy Tomi kettest, ötöst és hatost dobott, de nem ismerjük a dobások
sorrendjét.
a) Melyik szám melletti pontra juthatott el „Lajos” a
harmadik dobás után?
b) Melyik számra semmiképpen sem juthatott el a bolha a
játék folyamán?
-
Az összes számjegy (0-tól
9-ig) és két tizedesvessző segítségével írj fel két tizedes törtet úgy, hogy
összegük a lehető legkisebb legyen! Keresd meg az összes megoldást!
(Mindegyik számjegyet pontosan egyszer használhatod fel.)
-
Hófehérke hét törpéje az
erdőben gombát gyűjtött. Amikor hazaértek, kosaraikban egyenként 34, 19, 50,
44, 31, 28 és 37 gomba volt. Hófehérke megkérte őket, hogy néhány kosarat az
éléskamrába, néhányat a tűzhelyhez és a többit az asztalra helyezzék úgy,
hogy mindenhol ugyanannyi gomba legyen. A törpék úgy határoztak, hogy a
gombákat a kosarakban hagyják. Sikerül nekik Hófehérke kérése szerint
elhelyezni a kosarakat? Keress legalább egy megoldást!
-
Az ábra négyzetrácsában a
2007-es,szám látható. Határozd meg a sötét rész területét, ha a kis négyzet
oldalhossza 4 cm!

|
