Egy bogár egy négyzetrács közepébe esett. Elhatározta, hogy „spirálszerűen“ fog mászni, ahogy az ábrán látható; egyik négyzeten sem lesz kétszer és egy négyzetet sem fog kihagyni.

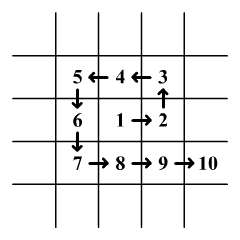
Az első négyzetről a másodikra kelet felé mászott, a másodikról a harmadikra északra, a harmadikról a negyedikre nyugatra, a negyedikről az ötödikre szintén nyugatra, az ötödikről a hatodikra délre, ... Milyen irányba mászott a 81.-ik négyzetről a 82.-ikre?

Misi egy papírból kivágott két egyforma négyzetet, egy 10 cm x 24 cm téglalapot és még egy téglalapot. Milyen lehetett ez a téglalap, ha ebből a négy darabból össze lehetett rakni egy négyzetet úgy, hogy az egyes darabok fedjék egymást? Ilyen téglalap több van, találj legalább négyet.

Találd meg az összes megoldását a következő algebrogrammának. Az egyforma betűket helyettesítsd egyforma számokkal, a különbözőket különbözőkkel.

Nóri a tanító nénitől a következő kártyákat kapta:

Ezekből kell összeállítania egy feladatot az osztálytársai részére úgy, hogy minden kártyát éppen egyszer használ. Segíts Nórinak és szerkessz egy ilyen feladatot úgy, hogy minden osztás maradék nélkül jöjjön ki. Milyen lesz az eredmény?

84 diákunk moziba ment. Egy jegy ára 2 € volt, de minden 12.-ik diák féláron és minden 35.-ik ingyen mehetett moziba. Mennyibe került a belépődíj az összes diák részére?

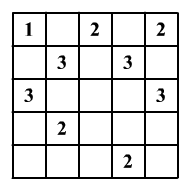
A fiúk egy régi aknamező tervrajzát találták meg (lásd az ábrát). A számok azokon a mezőkön vannak, amelyeken nincs akna és az aknát tartalmazó szomszédos mezők számát jelzik. Határozd meg, hány akna van összesen és melyik mezőkön vannak. (A mezők akkor és csak akkor szomszédosak, ha van közös oldaluk vagy csúcsuk.)