|
|
|
Matematikai Olimpia, 5. évf., 2003/04, I. ford. feladatai
-
Az olyan többjegyű számot,
melynek számjegyei balról jobbra haladva növekednek (az egyesek száma
nagyobb, mint a tízesek száma, a tízesek száma nagyobb, mint a százasok
száma, a százasok száma ...) növekvő számnak hívjuk. Például
a 2459 egy növekvő szám, de a 2354 nem növekvő szám.
Az összes létező növekvő számot sorba rendeztük, a legnagyobbtól
a legkisebbig, és közülük az első tízet összeadtuk. Milyen
eredményt kaptunk, ha helyesen számoltunk?
-
Az ábrán látható
alakzatot gyufaszálakból raktuk ki.
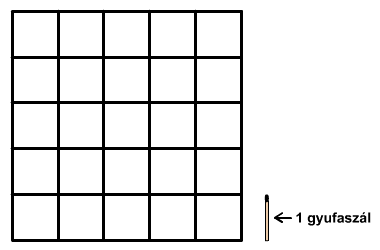
a) Hány gyufaszálat használtunk fel?
b) Hány gyufaszálat kell elvenni az eredeti ábrából
úgy, hogy pontosan 12 darab olyan négyzet maradjon, amelyek csak csúcsaikban
érintkezhetnek egymással? (A négyzet oldala = 1 gyufaszál.)
Rajzold le az így létrejött ábrát!
-
A tudósok egy új gyümölcsfát
nemesítettek ki és a KÖRTALMAFA nevet adták neki. Egy ilyen fán körték
és almák is teremnek egyszerre, de más gyümölcs nem. Ugyanakkor
mindig kétszer annyi alma terem rajtuk, mint körte. A KÖRTALMAFÁRÓL
még azt is tudjuk, hogy évente nem terem rajta 77-nél kevesebb, de
88-nál több gyümölcs sem.
a) Legalább hány almát terem egy KÖRTALMAFA
évente?
b) Teremhet-e 55 KÖRTALMAFÁN egy év alatt 1600
db körte?
-
A 3256871 és
a 4589238 számokból, amelyek együtt 14 számjegyből állnak,
húzzatok ki összesen 5 számjegyet úgy, hogy a megmaradt számok összege
a lehető legkisebb legyen!
-
Ha két téglalap összebarátkozik,
oldalaik mentén úgy simulnak egymáshoz, hogy legalább egy közös
csúcsuk legyen.
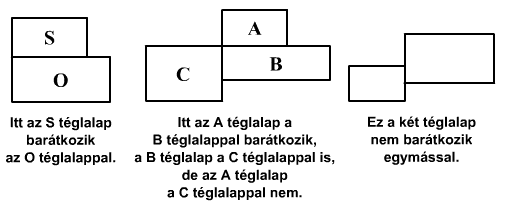
A 6 cm oldalú négyzet összebarátkozott a 7 cm x 9 cm
méretű téglalappal. Később találtak még egy négyzetet,
amellyel mindketten összebarátkoztak. Milyen méretű lehetett ez a
négyzet? Keresd meg az összes lehetőséget! (A négyzet a téglalap
speciális esete, és rá is ugyanaz a barátkozási feltételek érvényesek,
mint a téglalapra.)
-
Gondoltam egy számot. Tízezresekre
való lekerekítése után a 20000 számot kapom. Az általam gondolt
szám tízesekre való kerekítéssel nem változik, ezresekre való
kerekítéssel 20-szal növekszik, százasokra való kerekítéssel
szintén 20-szal növekszik. Milyen számra gondoltam? Írd le az összes
lehetőséget!
|
