|
|
|
Matematikai Olimpia, 5. évf., 2000/01, II. ford. feladatai
-
Ha Vilmos lépeget az iskolába,
27 lépést tesz meg. Ha ugrál, 18 ugrás az iskola. Ma kitalálta,
hogy felváltva 2 lépést megy előre, és egy ugrást hátra, míg
nem ér az iskolába. Hány lépést kell mennie és hányat ugrania,
hogy ma iskolába jusson? (Az összes lépés egyforma hosszú. Az összes
ugrás egyforma hosszú.)
-
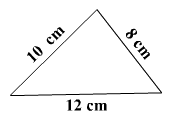
Hány ilyen háromszögből
tudunk egy 56 kerületű négyszöget összerakni? Rajzold le az
összes lehetőséget ahogy a négyszög kinézhet. (A háromszögek
nem fedhetik egymást.)
-
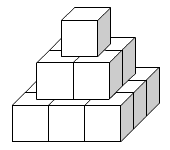
A piramis alsó sora kockáin
különböző páros természetes számok vannak felírva. A felírt
számok összege 100. A többi kockán azon kockák számainak az összege
van, amelyen a kocka áll. Milyen legkisebb szám lehet a legfelső
kockán?
|
