|
|
|
Matematikai Olimpia, 7. évf., 2009/10, I. ford. feladatai
-
Egy
borszaküzletbe éjszaka bejutott egy kandúr. Felugrott a polcra,
amelyen hosszú sorban egymás mellett álltak a borosüvegek – az első
harmadban 8 € üvegenként, a következő harmadban 6,5 € üvegenként
és az utolsó harmadban 5 € üvegenként. Először a kandúr a sor szélén
lévő 8 €-s üveget lökte le, utána egyet sem kihagyva egymás után
lökdöste le az üvegeket. A kandúr ezt akkor hagyta abba, amikor 25
üveget lökött le és ezek mind széttörtek. Reggel a tulajdonos azon
bánkódott, hogy a kandúr nem a polc másik széléről kezdte az üvegek
lelökését. Még ha ugyanannyi üveget is tört
volna el, a kár 33 €-val kisebb lenne.
Hány üveg volt eredetileg a polcon?
-
Legyen
a, b, c egy táblára felírt olyan három természetes szám,
amelyekre érvényes:
• az a, b számok legnagyobb közös osztója
15,
• a b, c számok legnagyobb közös osztója
6,
• a b, c számok szorzata
1800,
• az a, b számok legkisebb közös többszöröse
3150.
Melyek ezek a számok?
-
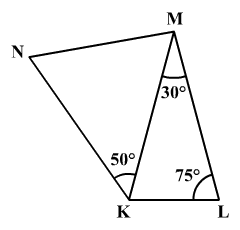
A KLMN négyszögben ismerjük a kijelölt szögeket és tudjuk,
hogy |KN| = |LM|.
Határozd meg milyen nagy a KNM szög.
-
Egy kocka 64 darab 2 cm élű kis kockából állt. Azután a kocka
látható részéből eltávolítottunk néhány kis kockát, lásd az ábrát.
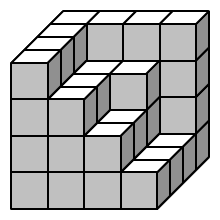
a) Határozd meg ennek az idomnak a térfogatát és a felületét..
b) Ennek
az idomnak az egész felületét pirosra festettük, azután szétszedtük
az eredeti kis kockákra.
Hány kis kockának volt 6, hánynak 5, 4, 3, 2, 1 ill. 0 piros fala?
-
A számegyenesen meg van jelölve két szám: a
12x és a –4x.
Jelöld meg ezen a számegyenesen a nullát
és az x számot.
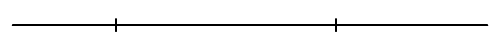
-
A csillagok helyett írj számokat úgy, hogy a két feladat
eredményének összege 5842 legyen.
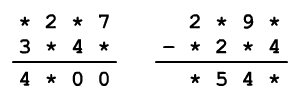
A feladatnak több megoldása van, találj legalább kettőt.
|
