Az én mamám 1948.3.16.-án született. Ez szép dátum, mert igaz rá hogy  48 = 3 . 16 . A 20. század melyik éveiben volt a legkevesebb ilyen szép dátum? Keressétek meg az összes megoldást.

Dominik gyurmával játszott, melyből elkészített egy   6 cm  x  3 cm  x  19 cm   méretű téglalatestet. Ezután szétnyomta és ebből a gyurmából elkészített három különböző méretű kockát. Nagy meglepetéssel tapasztalta, hogy mindegyik kocka élének hossza centiméterekben kifejezve egész szám volt. Milyen méretei voltak Dominik kockáinak?

Egy természetes szám vidám, ha osztható 9-cel vagy 13-mal, szomorú, ha osztható 12-vel, éhes, ha tartalmaz legalább egy nullát, kicsi, ha kétjegyű és nagy, ha 200-nál kisebb háromjegyű szám. Milyen nagy lehet a területe annak a téglalapnak, melynek szélessége kicsi, szomorú, éhes; hosszúsága nagy, vidám, éhes és kerülete szintén éhes?

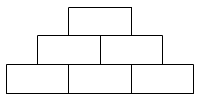
Írj be az ábrán látható "szorzatpiramis"-ba természetes számok úgy, hogy a legnagyobb beírt szám a 315 legyen és semmelyik két beírt szám ne legyen egyenlő. Hány különböző képpen lehet ezt megtenni? (A "szorzatpiramis"-ba beírt bármelyik szám egyenlő az alatta levő két szám szorzatával.)

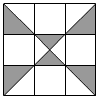
Iván egy különleges fehér-barna csokoládét kapott (lásd árba). Határozd meg a fehér rész tömegét, ha az egész csokoládé három egyenlő széles sorból és három egyenlő széles oszlopból áll és az egész csokoládé tömege 144 gramm.

Három dalmata és 2 spicc tömege annyi, mint 14 tacskó tömege. Egy dalmata tömege annyi mint 1 spicc és 3 tacskó tömege. Hány tacskó tömege egyenlő 101 dalmata tömegével? (A kutyák egy fajon belül egyenlő súlyúak.)