|
|
|
Matematikai Olimpia, 6. évf., 2007/08, II. ford. feladatai
-
Kozel úr kertjében néhány
cseresznyefa virágzott. Mindegyik cseresznyefán három rigó ült, egy
pedig a kerítésen. Kozel úr kutyája rajuk ijesztett és a rigók
elrepültek. Kevés idő elteltével a rigók mind visszatértek és a
cseresznyefákra ültek. Az a cseresznyefa, amelyik alatt a kutya
aludt, üresen maradt, a többi fa mindegyikére négy rigó ült. Hány
cseresznyefája van Kozel úmak és hány rigó volt a kertjében?
-
Adott az ABC háromszög,
amelyben a C pontból az AB egyenesre bocsátott merőleges
P
talppontja az AB szakasz belsejében van. Legyenek
p, q a P pontból
az AC illetve a BC egyenesekre bocsátott merőlegesek (adott
sorrendben). Legyen továbbá S a BC és
q egyenesek metszéspontja,
valamint T az AC és p egyenesek metszéspontja. Számítsd ki az
ACB
szög nagyságát, ha tudod, hogy APT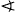 +
BPS +
BPS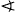 =
20°. =
20°.
-
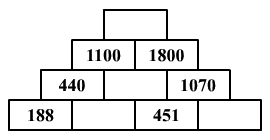
Az ábrán egy kerekítős
összeadós piramis látható. Minden téglában (a legalsó sort kivéve)
az alatta lévő két szomszédos téglába írt szám összege található, de
sornak megfelelően kerekítve: az összeget alulról a második sorban
tízesekre, a harmadik sorban százasokra, a legfelső, negyedik sorban
ezresekre kerekítjük. Írd be a piramis üres tégláiba a lehető
legnagyobb egész számokat.
|
