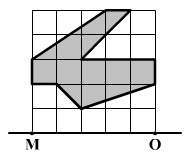
Az ábrán egy négyzetháló látható, amelyen a négyzetek oldala 1 cm hosszú. A négyzethálóban egy szürkére festett alakzat található. Libornak olyan egyenest kell szerkesztenie, amely párhuzamos az MO egyenessel és a szürke alakzatot két egyenlő területű részre osztja. Az MO egyenestől milyen távolságra rajzolja Libor ezt a párhuzamost?

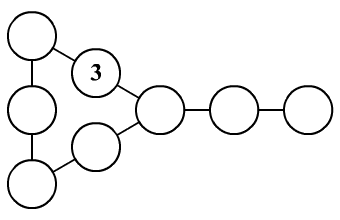
Az üres mezőkbe írd be a 2, 4, 6, 8, 12, 14 és 21 számokat úgy, hogy minden egy szakaszra írt 3 szám azonos szorzatot adjon. Írd le a megoldásod menetét!

A Bé-bank olyan négyjegyű PIN-kóddal ellátott kártyákat ad ki, amelyek nem tartalmazzák a 0 számjegyet. Szklerózis úr félt, hogy elfelejti a kártyája PIN-kódját, ezért ráírta azt egyenesen a kártyára. Hogy az esetleges tolvajnak ne legyen olyan könnyű dolga, római számokkal írta: IIIVIIIXIV. Ezt az ötletet elárulta legjobb barátjának, Leső úrnak. Neki úgy megtetszett az ötlet, hogy a saját PIN-kódjával ugyanezt tette és helyesen ráírta a kártyára: IVIIIVI. Legnagyobb meglepetésére azonban nem tudta a leírt római írásmódból a PIN-kódját pontosan visszaolvasni.
a) Milyen PIN-kódja van Szklerózis úr kártyájának?
b) Milyen PIN-kódja lehet Leső úr kártyájának?

Vázold fel az összes lehetséges különböző alakú négyszöget, amelyeknek csúcsai egy adott szabályos hatszög csúcsaiban vannak elhelyezve. Mekkora lenne a területük, ha a hatszög területe 156 cm² lenne?

Kucsera asszony hétnapos nyaralása alatt Kati sétáltatta a kutyáját és etette a nyulait. Kati ezért egy nagy tortát és 700 koronát kapott. A következő négynapos nyaralás alkalmával azonos szabály szerint egy ugyanolyan tortát és 340 koronát kapott. Mennyibe került a torta?

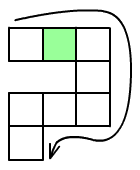
Egy kocka minden lapjára más-más 20-nál kisebb törzsszámot (prímszámot) írtunk úgy, hogy a szemben fekvő lapokon levő számok összege mindig ugyanannyi legyen. A kockát ráhelyeztük az ábrán látható játéktábla első mezejére a legkisebb számmal lefelé fordulva és a nyílnak megfelelően gurítottuk. Minden esetben, amikor a kocka lapja érintkezett a játéktáblával, az érintett mezőbe beírtuk az azt érintő lapon levő számot. Milyen számú lap érintette a kiszínezett mezőt, ha a beírt számok összege a lehető legkisebb volt? (A játéktábla olyan négyzetekből áll, amelyek a kocka lapjaival egybevágóak.)