A 6574839201 számból hagyjál ki számjegyeket úgy, hogy az így keletkezett szám minél kisebb legyen, a tízesek és az ezresek helyén álló számjegyek összege 7 a százasok és az egyesek helyén álló számjegyek  különbsége pedig 2 legyen.

A JURO téglalap kerülete 36 cm, a LENA négyzet kerülete pedig 24 cm. JURO és LENA az olyan téglalapok és négyzetek szülei, amelyeknek a kerülete LENA vagy JURO kerületének a fele. Közben, minden leány négyzet és egyetlen fiú se négyzet. Határozzátok meg JURO és LENA különböző fiainak és leányainak legnagyobb számát, ha a gyerekek méretei centi-méterekben adva egész számok.

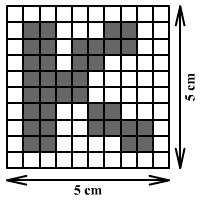
Katikának K betűmintával sálat kötött a nagymamája. Először egy négyzet alakú mintát kötött amely oldalának hossza 5 cm (ábra). Azután az ilyen mintákból 1 m hosszú és 20 cm széles sálat készített. Hány K betű volt a sálon?

Hétfőtől péntekig a Bobi kutyánk egyedül van otthon, mert a szülők munkában és a gyerekek iskolában vannak. Az egyik hónapban viszont csak 11 napot volt egyedül. Először három napot, vasárnaptól keddig Ivánnal volt, mert Ivánnak fájt a hasa. Meggyógyulása után rögtön Majka náthalázzal maradt otthon, szerdától a következő hét csütörtökéig. Hány napja lehetett  ennek a hónapnak?

A karácsonyi vásáron 5, 7 és 9 karú gyertyatartók voltak, minden karba egy gyertya volt elhelyezve. Összesen 9 gyertyatartó és 67 gyertya volt. Határozd meg, hogy a különböző gyertyatartókból hány darab volt.

A tornaórán 9 fiú és 8 leány van két oszlopsorba felsorakoztatva. A fiúk oszlopsorában minden fiú 1 cm-rel magasabb az előtte állónál, a leányok oszlopsorában pedig minden leány 2 cm-rel magasabb az előtte állónál. A legmagasabb leány 15 cm-rel magasabb, mint a legalacsonyabb fiú. A harmadig legmagasabb fiú magassága 134 cm. Hány cm a magassága a legalacsonyabb leánynak?