A jelek helyére írj számjegyeket úgy, hogy a számítás helyes legyen:

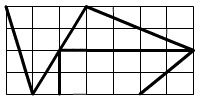
Tintácska, Földecske, Eperke, Borsócska és Napocska manók találtak az erdőben egy elhagyott csokoládét. Széttördelték darabokra ahogy az ábra mutatja, és elkezdték megenni. A legnagyobb részt Borsócska ette meg. Napocska és Tintácska ugyanannyit evett, de Napocska három részt evett meg, Tintácska csak egyet. Földecske megette a csokoládé hetedét, a maradékot pedig Eperke ette meg. Mindegyik törpéhez színezd ki a törpe színével a csokoládé azon részét, amelyet megevett.

Az ábrán a számegyenes egy részét látod. Írd be a felhőcskékbe a számokat, ha tudod:
  •  A beírt számok közül három darab osztható 4-gyel maradék nélkül.
  •  Egyik szám sem nagyobb mint 111, se nem kisebb mint 94.

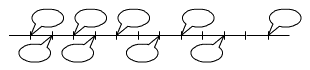Az anyuka szeretne Milka kabátjára rávarrni 4 gombot. Összesen van 5 sárga, 2 rózsaszín és 1 kék színű gombja. Milka azt kérte, hogy a kabátján ne legyen egymás fölött két egyforma színű gomb, és legalább az egyik szélső gomb sárga legyen. Hány különböző képpen varrhatja fel anyuka a gombokat, ha szeretné teljesíteni Milka kérését? Rajzold le az összes ilyen kabátot.

A papíron ábrázolva vannak az A, B, C, D, X és Y pontok úgy, hogy igaz rájuk:
  •  A, X, Y és D pontok egy téglalap csúcspontjai.
  •  X, B, C és Y pontok egy téglalap csúcspontjai.
  •  Az ABCD négyszög területe 15 cm².
  •  Az AXYD téglalap területe kétszer akkora, mint az XBCY téglalapé.
  •  Az AB szakasz hossza 3 cm.
Számítsd ki az AXYD téglalap területét és kerületét.

Misinek vannak számkártyái a 0, 1, 2, 3, 4, 5, 6, 7, 8 és 9 számjegyekkel. (Minegyik csak egyszer.) Ezekből a kártyákból kirakott három háromjegyű számot. Az első szám számjegyeinek összege 13, a másodiké 14 és a harmadiké 15. Milyen legkisebb eredményt kaphatott Misi, ha összeadta a három háromjegyű számot?