Az 53 827 és 19 763 számokból hagyj ki összesen két számjegyet úgy, hogy az így kapott számok összege a lehető legnagyobb legyen!

Narancsos üdítő elkészítéséhez szükséges hozzávalók: 8 narancs és 2 citrom leve, 2 teáskanál cukor, 6 deciliter víz. Egy kancsóba 9 deciliter vizet öntöttünk. Hány narancs és hány citrom levét, és hány teáskanál cukrot kell még hozzáadnunk, hogy a receptben leírt minőségű üdítőt kapjuk?

Palinak és Annának egy 70 lécből álló fakerítést kellett befesteniük. A munkát együtt kezdték és együtt is fejezték be. Anna 4 perc alatt 2 lécet festett be, Pali 8 perc alatt 3 lécet tudott befesteni. Hány perc alatt végeztek a munkával?

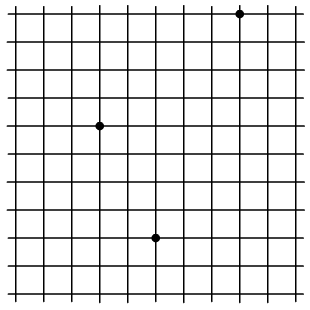
Az alábbi ábrán egy négyzetrács része látható, amelyben három rácspontot jelöltünk ki (elnevezésüket – sajnos – valaki kitörölte). E három pont közül tetszőleges két ponthoz találhatunk olyan négyzeteket, amelyeknek két csúcsát ez a két pont képezi. Az így létrehozható összes négyzet közül a KAMI négyzet a legkisebb. Rajzold be a négyzetrácsba a KAMI négyzetet!

Marci és Zsuzsi összehasonlították Mikulás-napi csomagjaikat, amelyek kedvenc csokoládéjukat is tartalmazták. Mivel a csokoládék száma a két csomagban nem egyezett, ezért a jószívű Marci csokijainak negyedét Zsuzsinak ajándékozta. Zsuzsi megszámolta hány csokija van és a felét visszaadta Marci barátjának. Erre Marci csokijainak negyedét ismét Zsuzsinak ajándékozta. Ezután jöttek rá, hogy mindkettőjüknek 9-9 csokoládéja van. Hány csokoládéja volt eredetileg Marcinak és mennyi Zsuzsinak? (Az ajándékozás és számolás közben egyetlen csokoládét sem ettek meg.)

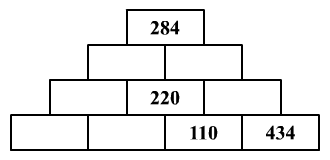
Az ábrán látható számpiramis minden mezőjében (kivéve a legalsó sor mezőit) az alatta levő két mezőbe írt számok összegének fele szerepel. Írd be a megfelelő számokat a számpiramis üres mezőibe!