|
|
|
Matematikai Olimpia, 6. évf., 2000/01, I. ford. feladatai
-
Egy ötjegyű szám a következő
tulajdonságokkal rendelkezik:
• a második számjegye az első számjegyének és
az első számjegyének a szorzatával egyenlő;
• a negyedik számjegye egyenlő a második és a
harmadik számjegyének a szorzatával;
• az ötödik számjegye egyenlő a második és a
negyedik számjegyének a hányadosával.
Határozd meg az összes ilyen tulajdonságú számot.
-
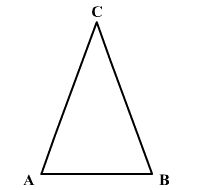
Írd le, hogyan lehetne csak
körző felhasználásával meggyőződni arról, hogy az
ábrán látható háromszög egyenlő szárú, és ACB szárszöge
40°.
-
A téglatest éleinek hossza
centiméterekben egész számokkal van kifejezve. Két lapja területének
a nagysága 147 cm2 és 539 cm2. Mekkora
lehet a téglatest térfogata?
-
A 6.A osztály
fizikajegyeinek átlaga a félévben 1,7 volt. Az év végén Matyi
2-ről 1-re, Ivanka 3-ról 2-re, Elenka 4-ről 2-re javított,
míg Palkó 3-ról 4-re rontott. Ennek következtében az osztály átlaga
0,1-del javult. Legfeljebb hány gyereknek lehetett a 6.A osztályban
az év végén egyese fizikából?
-
Ha egy kétszámjegyű szám
számjegyei közé az 51-et iktatjuk, akkor 7-tel osztható számot
kapunk. Ha 51 helyett a 15-öt tennénk, akkor 5-tel osztva 2 maradékot
kapunk. Határozd meg az összes ilyen tulajdonságú kétjegyű
számot.
-
Münchhausen báró néhány
konvex sokszöget rajzolt és azt állította, hogy van közöttük
olyan négyszög, amely három hegyesszöggel rendelkezik, továbbá
olyan ötszög és hatszög, melyeknek négy-négy hegyesszögük van.
Hány esetben lehetett igaza a bárónak? Magyarázd meg, hogy miért.
|
