|
|
|
Matematikai Olimpia, 6. évf., 2009/10, I. ford. feladatai
-
Jancsi és
Juliska a nagymamához járnak, akinek van egy cukrászdája és
mézeskalácsot árul. Mindkét gyerek természetesen segít a
nagymamának, főleg a mézeskalács díszítésével. Amíg a nagymama öt
mézeskalácsot díszít, addig Juliska hármat és Jancsi kettőt. A
legutóbbi látogatásnál mindhárman összesen öt teljes tálca
mézeskalácsot díszítettek. Juliska a nagymamával az egész idő alatt
díszítettek, Jancsi eleinte díszített, később minden tálcára
tizenkét mézeskalácsot rakott és hordta a tálcákat a kamrába.
Mindhárman egyszerre kezdték a munkát és egyszerre is fejezték be.
a) Hány mézeskalácsot díszített Jancsi?
b) Mennyi ideig tartott nekik a munka, ha a nagymamának 4 percet
tart egy mézeskalács díszítése?
c) Mennyi ideig segített Jancsi díszíteni?
-
Robi
mobiljának négyszámjegyű PIN-kódja nagyon érdekes:
• a számjegyei prímszámok,
• az első és második számjegy
(ebben a sorrendben) prímszámot alkot,
• a második és harmadik számjegy
(ebben a sorrendben) prímszámot alkot,
• a harmadik és negyedik
számjegy (ebben a sorrendben) prímszámot alkot,
Robi elfelejtette a PIN-kódot, de ismeri az összes fent említett
tulajdonságot és igyekszik üzembe hozni a kikapcsolt mobilt. Milyen
számokat kellene kipróbálnia?
-
A következő
ábrán hét egyforma négyszögből álló idom van. Mennyi ennek az
idomnak a kerülete, ha egy négyszög kerülete 17 cm?

-
Apu
elhatározta, hogy Marci fiának minden hónapban egyszer zsebpénzt fog
adni. Az első zsebpénzt Marci januárban kapta. Apu minden hónapban 4 €-val
emelte a zsebpénzt. Ha Marci nem költekezne, akkor a 12.-ik zsebpénz után karácsony előtt lenne 900 €-ja. Hány
€-t kapott Marci januárban első zsebpénzként?
-
A csillagok helyett írj számokat úgy, hogy a két feladat
eredményének összege 5842 legyen.
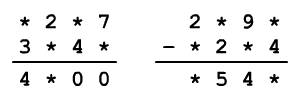
-
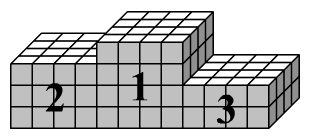
Az iskolai olimpiára a diákok fakockákból dobogót
készítettek, lásd az ábrát. Hány kockát használtak összesen?
Az összeállított dobogó egész felületét (az alján kívül) fehérre
festették és az eredményhirdetés után a dobogót szétszedték.
Hány kockának volt 6, hánynak 5, 4, 3, 2, 1 ill. 0 fehér fala?
|
