|
|
|
Matematikai Olimpia, 6. évf., 2006/07, II. ford. feladatai
-
Egybevágó szürke
háromszögekből és hat egybevágó négyzetből alkottunk egy alakzatot.
A közepén (egymás fedése nélkül) elfér három egybevágó négyszög,
melyek területe 4 cm2.
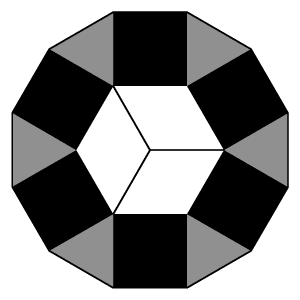
a) Határozzátok meg a szürke háromszögek belső szögeinek nagyságát.
b) Határozzátok meg az egész szürke felület területét.
-
Cyrilnek a negyedével több
golyója van, mint Borisnak. De Borisnak a negyedével több van mint
Ádámnak. Együtt 122 golyójuk van. Hány golyója van Cyrilnek,
Borisnak és Ádámnak külön-külön?
-
Egy többjegyű számot
optimista számnak nevezünk, ha a számjegyek balról jobbra
növekednek. Ha a szám számjegyei balról jobbra csökkennek, akkor azt
pesszimista számnak nevezzük. Ugyanazokból a számjegyekből alkotott
pesszimista és optimista szám összege 109900, különbsége 84942.
Melyek ezek a számok?
|
