|
|
|
Matematikai Olimpia, 6. évf., 2003/04, I. ford. feladatai
-
Cikcakk számnak
nevezzük az olyan természetes számot, amelyben váltakoznak a páros
és páratlan számjegyek, és a számjegyek közül semelyik kettő
nem azonos. Ha az összes cikcakk számot rendezzük a
legnagyobbtól a legkisebbig, melyek lesznek sorrendben az 1., 5., és
a 10. helyen?
-
A tanár úr elkészítette a
kocka, a tetraéder és a szabályos négyoldalú gúla drótmodelljét
(ábra). Mindhárom test élei egyenlő hosszúak és cm-ben mért
nagyságuk egész számmal fejezhető ki. A kocka elkészítéséhez több
mint 45 cm drótra volt szüksége, a gúlához kevesebb mint 35 cm
is elég volt. Pontosan hány cm drótra volt szüksége a tetraéder
elkészítéséhez?
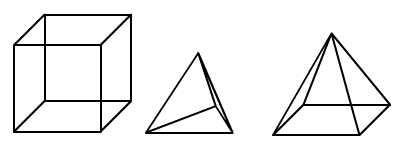
-
Piroska vonattal utazik a
nagymamához. Rendszerint a 9:23-kor induló gyorsvonatra száll fel,
és 153 perc múlva kiszáll egy állomáson, ahol a személyvonat
csatlakozásra várakozik. Ma a gyorsvonat 12 perc késéssel indult
ki Piroska lakhelyéről. Ezt a késést a gyorsvonat még kétszeresére
növelte, de később 15 perccel csökkentette. Így Piroskának a
személyvonat rendes indulásáig csak 7 perc ideje maradt. A
menetrend szerint pontosan hány órakor kellene indulnia a személyvonatnak?
-
Írd le az alábbiak szerint
az összes egymás után következő számot 1-től 60-ig:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 ... 57 58 59 60.
Az így létrejött számból húzzál ki 100 számjegyet úgy, hogy a
megmaradt szám a lehető legnagyobb legyen!
-
A 27 cm x 12 cm
méretű téglalapot úgy oszd fel:
a) három téglalapra
b) két részre,
hogy belőlük négyzetet lehessen összerakni! (Az egyes részek nem
fedhetik egymást.)
-
A négyzethálós papíron
egy bábbal a következő szabályok szerint lépkedek: Gondolok egy
számot, azt elosztom kettővel. Ha a maradék 0, a bábot egy négyzettel
följebb tolom. Ha a maradék más, a bábot 1 négyzettel jobbra
tolom. A báb eltolása után a hányadost újból elosztom kettővel,
ezután a bábbal az előbbi szabályok alapján lépek és folytatom
a játékot tovább.
a) Kiválasztottam a 89 számot. Ábrázold a
báb első öt lépését ebben az esetben és írd le az utolsó hányadost!
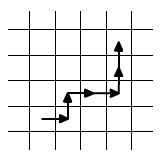
b) A bábbal úgy lépkedtem, ahogy az ábra
mutatja. A megtett lépések után hányadosul 1-et kaptam. Milyen számot
választottam az elején?
|
