|
|
|
Matematikai Olimpia, 6. évf., 2002/03, I. ford. feladatai
-
A hét törpe középiskolai felvételi vizsgára készül. A törpék helyesírásból Hófehérkétől vesznek leckét. Az első tollbamondásban a törpék átlagosan 35 hibát vétettek. A másodikban Vigyor már 15-tel kevesebb hibát vétett, mint az elsőben, Szundi viszont 13-mal többet, és Kuka is 2-vel többet. Hapci javult, mert másodszor 9-cel kevesebb hibát vétett és Tudor is 19-cel kevesebbet! A törpék közül kettő a második tollbamondásban ugyanannyi hibát vétett, mint az elsőben. Átlagosan hány hibát vétettek a törpék a második tollbamondásban?
-
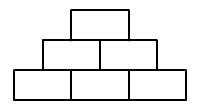
Töltsétek ki számokkal az ábrán látható "összeadásos" piramist úgy, hogy a beírt számok között szerepeljenek a következő számok is: -1,2 ; 2,3 ; -3,4 és emellett a legfelső szám
a) a lehető legnagyobb,
b) a lehető legkisebb legyen!
-
Buba 32 gyufaszálból egy olyan téglalapot rakott ki, amelynek oldalai nem egyformák. Ezt a téglalapot Buba kishúga néhány további gyufaszállal pontosan 7 négyzetre osztotta fel.
Hány gyufaszálból rakhatta ki Buba az eredeti téglalap egyes oldalait? A gyufaszálak hossza egyforma volt, és egyet sem törtek el.
-
Amióta csak megvették Novákék a két kutyakölyköt, Pöttyöt és Foxit, azóta minden nap egyszer sétára mentek. Néha Foxit vitték magukkal, máskor Pöttyöt, mindkét kutyát egyszerre azonban soha. Pötty eddig 14-szer maradt otthon, Foxi 16-szor. Tizennyolc esetben Novákék valamelyik kutyájukat magukkal vitték.
Hány napja vették meg Novákék a két kutyakölyköt?
-
A sárkánykészítők versenyén Ádám, Böske és Zsuzska bekerült a "Legszebb sárkány" díjért folyó küzdelem döntőjébe. A döntőben mind a 22 zsűritag minden versenyzőnek külön-külön 1, 2 vagy 3 pontot adott, egy-egy zsűritag mindhárom versenyzőnek más-más pontszámot adott. Ádám annyiszor kapott 3 pontot, ahányszor 1-et, 2 pontot néggyel több zsűritagtól kapott, mint 3 pontot. Böske
ugyanannyiszor kapott 3 pontot, mint Zsuzska, ugyanakkor 2 pontot Böskének kétszer annyi zsűritag adott, mint Zsuzskának. Melyikük lett a legtöbb ponttal a győztes, és a győztesnek hány pontja volt?
-
Karcsi dobozában 100 db fából készült, egyforma kocka volt, amelyeknek élhossza 1 dm. Karcsi a dobozban levő kockák egy részéből egy nagyobb kockát épített, és ennek a nagy kockának öt lapját befestette pirosra. Miután ledöntötte ezt a kockát, azokból a kis kockákból, amelyeket korábban a nagyobb kockánál felhasznált, egy hasábot rakott össze, mégpedig úgy, hogy a hasábnak is éppen öt lapja lett piros. Mekkora mérete volt a nagyobb kockának, és mekkorák a hasáb élei?
|
