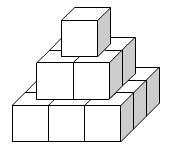
Az ábrán látható piramis természetes számokkal megszámozott kockákból áll. Az alsó szinten semelyik két kockának nincs ugyanolyan számja. A többi szinten levő kockák száma egyenlő az alatta levő 4 kocka számjainak összegével. Határozzátok meg, milyen legkisebb számja lehet a legfelső kockának, ha tudjátok, hogy a középső szinten levő kockák mindegyikének ugyanaz a számja van.

Van 4 egybevágó háromszögünk. Ezekből ki tudunk rakni (átfedés nélkül) nem csak olyan téglalapot, melynek kerülete 22 cm, vagy olyan téglapot amelynek kerülete 29 cm, hanem rombuszt is. Mennyi lesz a kerülete ennek a rombusznak? (Mindegyik kirakásnál fel kell használnunk mind a 4 háromszöget.)

A magánvállalkozó elbocsájtotta az alkalmazottjainak egy negyedét. Az ő munkájukat szétosztotta azok között, akik alkalmazásban maradtak, és ezek minegyikének megemelte a fizetését 25%-kal. Még így is megspórolt a béreken 13000 Sk-t. Határozzátok meg, hány alkalmazottat hagyott meg a cégnél, ha tudjátok, hogy mindegyik alkalmazott ugyanannyit keres (ugyanannyit keresett), és ez nem kevesebb mint 6000 és nem több mint 10000 korona.