Márton papírján olyan különböző számjegyekből álló ötjegyű szám szerepel, amely a következő tulajdonságokkal rendelkezik:
• balról a második (tehát az ezresek helyén levő) számjegy áthúzásával kettővel osztható számot kapunk,
• balról a harmadik számjegy áthúzásával olyan számot kapunk, amely osztható hárommal,
• balról a negyedik számjegy áthúzásával egy néggyel osztható számot kapunk,
• balról az ötödik számjegy áthúzásával egy öttel osztható számot kapunk,
• ha nem húzunk át egy számjegyet sem, akkor a szám osztható hattal.
Melyik az a legnagyobb szám, amelyik Márton papírjára van írva?

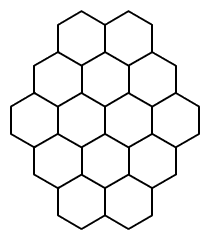
Károly az ábrán látható üres mezőkbe úgy igyekezett elhelyezni a természetes számokat 1-től 14-ig, hogy egyetlen számot se használjon fel többször és a számok összege minden egyenes sávban azonos legyen. Egy idő után észrevette, hogy ez nem lehetséges. Mivel indokolnátok Károly megfigyelését? (Egyenes sáv alatt mindazon szomszédos mezőket értjük, amelyek középpontja egy egyenesre esik.)

A „Rejtvények és fejtörők“ című enciklopédia ára 62,5%-kal csökkent. Matyi észrevette, hogy mindkét ár (az árleszállítás előtti és utáni is) kétszámjegyű és ugyanazokból a számjegyekből áll, csak más sorrendben. Hány euróval lett olcsóbb az enciklopédia?

Bontsátok kis egybevágó kockákra a 8 cm élű kockát úgy, hogy a felületük összege ötször nagyobb legyen, mint az eredeti kocka felülete. Mekkora lesz egy kis kocka térfogata és hány cm lesz egy élének a hossza?

Klári, Lenke és Matyi az írásbeli maradékos osztást gyakorolták. Az osztandó mindegyikük esetében más-más természetes szám volt, viszont mindegyikük osztója ugyanaz a természetes szám volt. Lenke osztandója 30-cal nagyobb volt, mint Klárié. Matyi osztandója 50-nel nagyobb volt, mint Lenkéé. Klári eredményében a maradék 8 lett, Lenke 2 maradékot, Matyi 4 maradékot kapott. Mindnyájan hibátlanul számoltak. Milyen osztóval számoltak a diákok?

Az egyenlő szárú ABCD trapézban az AC és DB átlók merőlegesek egymásra, hosszuk 8 cm, és a leghosszabb AB oldal szintén 8 cm-es. Számítsátok ki ennek a trapéznak a területét!