|
|
|
Matematikai Olimpia, 8. évf., 2006/07, I. ford. feladatai
-
Az 1-9 számjegyekből három
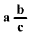 vegyes számot írtunk fel. Utána ezt a három számot összeadtuk. Mekkora a
legkisebb lehetséges összeg? (Mindegyik számjegyet pontosan egyszer
használtuk fel!)
vegyes számot írtunk fel. Utána ezt a három számot összeadtuk. Mekkora a
legkisebb lehetséges összeg? (Mindegyik számjegyet pontosan egyszer
használtuk fel!)
-
A király színültig töltette
boros serlegét és megitta a bor ötödét. Utána feltöltette a serleget vízzel
és megitta tartalmának negyedét. Ismét feltöltette vízzel és megitta a
harmadát. Végül a serleget még vízzel töltötték fel. A serleg térfogatának
hány százalékát teszi ki a végén az eredeti bor?
-
Adott az ABCDEFGHI szabályos
kilencoldalú sokszög. Számítsd ki a DG és BE egyenesek által bezárt szög
nagyságát.
-
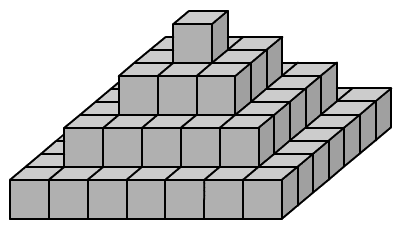
Az iskolában a diákok egy
halom egyforma kockából piramist építettek, amelynek egy része az ábrán
látható. Ez a piramis, amelyik a maga nemében a legnagyobb volt a világon,
az iskola udvarán állt és sajnos többször megázott. Ezért egy idő után ki
kellet cserélni az összes eső érte kockát (tehát a felületén lévőket).
Összesen 2025 kockát kellett kicserélni. Hány szintje volt a piramisnak?
-
A legelőn birkák legeltek.
Fele annyinak volt szarva, mint amennyinek nem. Sötétgyapjasból ugyanannyi
volt, mint világosgyapjasból.(Egyéb birka, mint egyszarvú, foltos stb. a
legelőn nem volt.) Csak három sötétgyapjas birkának nem volt szarva és a
világosgyapjasoknak egyáltalán nem volt szarvuk. Hány birka legelt a
legelőn?
-
Az ABC háromszög magassága két
részre osztja fel a háromszöget, amelyeknek területaránya 1:3.
Határozd meg az ABC háromszög területét és kerületét, ha
|AC| = |BC|
és |AB| = 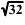 cm. cm.
|
