Az ábrán látható táblázatba írjatok egymástól különböző természetes számokat úgy, hogy a számok szorzata minden sorban, minden oszlopban és mindkét átló mentén külön-külön 1 000 legyen, ugyanakkor a számok összege az első sorban, és az első oszlopban a lehető legnagyobb legyen!

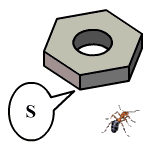
A hangya az ábrán látható anyacsavaron egy 1 cm oldalhosszúságú szabályos hatszög alakú pályán halad körbe-körbe, miközben 1 cm-t tesz meg 4 másodperc alatt. Milyen távol lesz az S kiindulási ponttól 2 és negyed perc múlva?

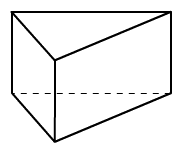
Az ábrán egy háromoldalú hasáb látható. Hány olyan háromszög létezik, amelynek mindhárom oldala e hasábnak éle vagy lapátlója?

A táborban 80 gyerek volt. Ezek a gyerekek 5 csoportot alakítottak ki. A vezető a csoportosítással nem volt elégedett, ezért az első csoportban lévő gyerekek egyötödét áthelyezte a másodikba. Ez még mindig nem volt egészen jó, ezért a második csoportban lévő gyerekek egyötödét áthelyezte a harmadik csoportba. Aztán a gyerekek egyötöde a harmadik csoportból átment a negyedikbe, majd a negyedik csoportban lévő gyerekek egyötöde átment az ötödikbe, végül az ötödik csoportból a gyerekek egyötöde csatlakozott az első csoporthoz. Így minden csoportban egyenlő lett a létszám. Hány gyerek volt az egyes csoportokban eredetileg?

Vektor kisasszony a következő feladatot adta Herminának: "Olyan napon és olyan hónapban születtem, amelyekre érvényes: ha a napot jelölő szám után leírom a hónap számát, megkapom születésem napjának sorszámát az évben (pl. a január 14. dátum a 141 számot adja, de ez a nap csak az év 14-dik napja, nem a 141-dik). Ha összeszorzod a születésem napját és hónapját, megkapod, hány éves lennék 2201-ben. Állapítsd meg, mikor születtem!" Ezt a faladatot oldjátok meg ti is!

Jutka szívesen küld mobiltelefonon SMS üzenetet. Naponta hármat elküld. Egy üzenet 2,50 koronába kerül. Több üzenet elküldése esetén az alábbi kedvezmények közül pontosan egyet választhat:
      10 SMS elküldése után 1 SMS-t küldhet ingyen,
    100 SMS elküldése után 10 SMS-t küldhet ingyen,
  1000 SMS elküldése után 100 SMS-t küldhet ingyen. 
Legalább mennyit fizet az elküldött SMS-ekért egy év alatt - az első elküldött SMS-től kezdve?