Misi gondolt egy háromjegyű számra. Gyurinak elárulta, hogy a gondolt szám számjegyeinek összege 8. Péternek csak a gondolt szám számjegyeinek szorzatát árulta el. Péter ebből helyesen meghatározta, hogy ilyen számból összesen 6 darab van és ezt elmondta Gyurinak. Ő kijelentette: "Már tudom, hogy milyen számjegyei vannak a számnak, de a szám meghatározásához ez még nem elég." Ezek után Misi mindkét fiúnak ezt mondta: "A második hatványa az utolsó számjegynek nem osztója a gondolt számnak." Ez már a fiúknak elég volt a szám meghatározásához. Milyen számra gondolt Misi?

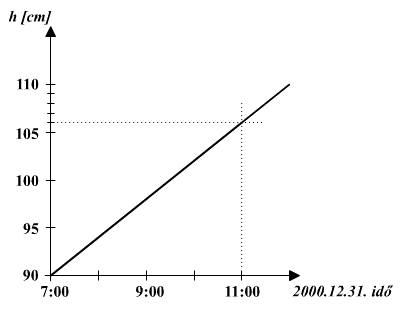
Pontban 2000.12.31.-ről 2001.1.1.-re eső éjfélkor akartak "Úszóváros"-ban ünnepélyesen megnyitni egy új, 160 cm mély téglatest alakú medencét. A vizet elkezdték engedni bele már 2000.12.30.-án. Az ábrán látható grafikon mutatja, hogyan növekedett a medencében a víz szintje az időtől függően.
a) Sikerült nekik időben teleengedni a medencét egészen a felső széléig?
b) Pontosan mikor kezdték el engedni a vizet a medencébe?

Az öreg farmer úgy döntött, hogy az összes vagyonát - egy csorda bárányt - szétosztja a gyerekei között. Először a csordát két részre osztotta 1:3 arányban. A kisebb részt odaadta elsőszülött fiának, a nagyobb részt ismét szétosztotta 1:3 arányban. Az új részekből a kisebbet odaadta másodszülött fiának, a nagyobb részt ismét szétosztotta 1:3 arányban. Ezt addig folytatta így, míg nem kapta meg az összes fiú a részét, majd a megmaradó részt odaadta egyetlen lányának. Határozd meg, hány fia volt a farmernak, ha csak egy kapott közüllük több bárányt, mint a farmer lánya.

Határozd meg, legfeljebb hány darab 100 mm átmérőjű labda fér bele egy téglalap alakú dobozba, melynek méretei 100 cm  x  100 cm  x  10 cm.

A teherautó első kerekein a gumiabroncsok 15000 km után használódnak el; a hátsó, dupla kerekeken 20000 km után. A sofőr éppen most vett hat új gumiabroncsból álló készletet. Legfeljebb hány kilométert tehet meg velük?

Az átlók 4 háromszögre osztják a 40 cm kerületű rombuszt. A háromszögek oldalainak hossza egész számok. Milyen legnagyobb kerülete lehet annak a
a) háromszögnek,
b) négyszögnek,
c) ötszögnek,
amelyet ezekből a háromszögekből rakhatunk össze? (A háromszögek nem fedhetik egymást és fel kell használnunk mind a 4 háromszöget.)