|
|
|
Matematikai Olimpia, 8. évf., 1989/90, III. ford. feladatai
-
Keressétek
meg azt a legkisebb, 72-vel osztható természetes számot, amely a
tízes számrendszerben felírva csak a 4 és 7 számjegyekből áll.
-
Szerkesszetek
legalább egy olyan egyenlő szárú háromszöget, amelynek területe
legalább 5 cm2
és minden magasságvonala rövidebb 2 cm-nél.
A megoldást indokoljátok.
-
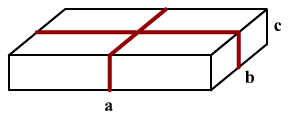
Az a,
b, c méretű (cm) bombonosdoboz az ábrán látható
módon van átkötve. A méretek egész számmal vannak kifejezve és
a > b > c .
A doboz térfogata
1764 cm3,
a szalag hossza (csomók és hurkok nélkül) 94 cm.
Számítsátok ki a doboz méreteit. Keressétek meg az összes megoldást.
-
Adott az
a = 6 cm
élű kocka. Az M pont a BF
meghosszabbításán, az F ponton túl, F-től
6 cm
távolságban található. Szerkesszétek meg a kocka metszetét az
ACM síkkal és számítsátok ki ezen metszet területét.
|
