Találjátok meg az összes ötjegyű 84-gyel osztható számot, amelyek a következő tulajdonságokkal rendelkeznek: az első három számjegy olyan számot alkot, amely háromszor nagyobb, mint a maradék két számjegyből álló szám. A számjegyek sorrendje azonos az ötjegyű szám számjegyeinek sorrendjével.

Mely  p  törzsszámra érvényes, hogy a  2p+1  valamely természetes szám harmadik hatványa?

A villamosvonal végállomásai közti menetidő 45 perc. A villamosok mindkét végállomáson 5 percet várnak. A villamosvonalon 5 szerelvény hozzáadásával a villamosok közti időköz egy perccel csökkent. Hány szerelvény és milyen időközökben közlekedik most a vonalon? (A percekben számolt időköz hossza természetes szám.)

Adott az ABC egyenlő szárú háromszög, |AC| = |BC|. A CB oldal B pont mögötti meghosszabításán válasszátok meg a D pontot úgy, hogy |BD| = |AB|. A BAC és BAD szögek tengelyeinek metszéspontjait a CD szakasszal jelöljétek E-vel és F-fel. Mekkora az EAF szög, ha CAB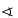= α ?

Adott a KLMN 6 cm oldalú négyzet. Szerkesszétek meg azt az ABC háromszöget, amely rendelkezik a következő négy tulajdonsággal:
  (1)  az A csúcs a KL egyenesen fekszik,
  (2)  a C csúcs a KN egyenesen fekszik,
  (3)  az M pont távolsága az A és C pontoktól 7 cm,
  (4)  |AB| : |BC| : |CA| = 1,5 : 2 : 1.
Hány megoldása van a feladatnak?

Adott az ABV egyenlő oldalú háromszög, |AB| = 8 cm. Szerkesszétek meg azt az ABCD téglalapot, amelynek CD oldala áthalad az AV szakasz K középpontján. Továbbá szerkesszétek meg a CD határegyenesű és A belső pontú félsíkban a CDU egyenlő oldalú háromszöget. Számítsátok ki az ABCD téglalap azon részeinek teljes területét, amelyek az ABV és CDU háromszögön kívül esnek.