Kaptam két természetes számot. Utána mindkettőt tízesekre kerekítettem. Milyen számokat kaptam, ha tudjátok, hogy érvényesek a következő állítások:
• a kerekített számok hányadosa ugyanolyan mint az eredeti számok hányadosa,
• a kerekített számok szorzata 295-el nagyobb mint az eredeti számok szorzata,
• a kerekített számok összege 6-al nagyobb mint az eredeti számok összege.

Pat és Mat kirándulni voltak. Reggel nyolc után indultak, amikor Pat óráján a kis és nagy mutató ellentétes félegyeneseken voltak. Ellentétes félegyeneseken volt Pat óráján a kis és nagy mutató akkor is, amikor a két barát délelőtt hazaért a kirándulásról. Mat stopper órával mérte, hogy mennyi ideig tartott a kirándulás. Tik is határozzátok meg másodperces pontossággal, hogy mennyi ideig tartott a kirándulás. Pat és Mat órái pontosak voltak.

Az ábrán egy 2 cm élű kocka van, amely nyolc 1 cm élű kis kockából áll. A kis kockák nyolc fala feketére van festve, a többi fal fehér. A kis kockákból összerakható olyan nagyobb kocka, amelyiknek felülete fehér. Hányféle képpen lehet a kis kockákat így befesteni? Az egyformán befestett kis kockákat nem tudjuk megkülönböztetni, tehát felcserélhetők.

Ádám és Éva 31 almát tartalmazó kosarat kaptak. Az első napon Éva a három negyedét ette meg annak, amit Ádám. A második napon Éva a két harmadát ette meg annak, amit Ádám megevett a második napon. A második nap estéjére a kosár kiürült. Hány almát evett meg Éva a kosárból? (Ádám és Éva egész almákat esznek és nem osztoznak rajtuk.)

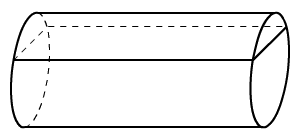
Egy henger alakú tartály hossza 4 m és az alapjának az átmérője 180 cm. Hány hektoliter tej van a tartályban, ha az átmérője három negyedéig van benne tej?

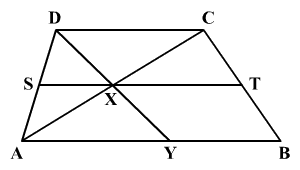
Az ABCD trapézban az AB és CD alapok hossza 7 cm és 4 cm. Az S ill. T pontok az AD ill. BC oldalak középpontjai, lásd az ábrát. Az X pont az AC és ST szakaszok metszéspontja, az Y pont az AB szakasz és DX egyenes metszéspontja. Az AYCD négyszög területe 12 cm². Számoljátok ki az ABCD trapéz területét.