|
|
|
Matematikai Olimpia, 9. évf., 1999/00, I. ford. feladatai
-
Adottak az ábra szerinti J, K, L, M, N pontok. Szerkessz AB átfogójú, derékszögű ABC háromszöget, ha a J, K, L, M, N pontok rendre az AB, BC, CA,
va, vc egyeneseken fekszenek, ahol va,
vc a megfelelő magasságokat jelölik.
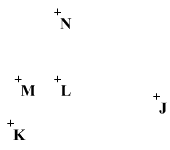
-
Határozd meg az abcd négyjegyű számot (a, b, c, d számjegyek), melyre igaz:
ab : bc = 1 : 3
bc : cd = 2 : 1
miközben ab, bc, cd kétjegyű számokat jelölnek.
-
Az AX, BY félegyenesek az ABC háromszög CAB és ABC szögeit 1:2 arányban osztják, és az ABC háromszög köréírt körének középpontjában metszik egymást. Határozd meg a háromszög szögeit!
-
Nevesincs országban nincsenek pénzérmék. De azért van automata gépük, amely az érméket papírpénzre váltja. Első lépésként az automata a bedobott összeget tízesekre kerekíti. Az így kapott értéket százasokra kerekíti, majd azt még ezresekre. Ezután a kapott összeget papírpénzben adja ki. Jancsi méregbe gurult, mert az automata alaposan megtréfálta. Ő a gépbe szórta egész vagyonát, az viszont csak körülbelül a 69%-át (egész értékre kerekítve) adta vissza annak, amit beledobott. Hány Nevesincs koronát dobott a gépbe
Jancsi?
-
Az ABCDE hatlap az ABCD és ABCE tetraéderek összeragasztásával keletkezett. A hatlap minden lapjára egy számot írtunk. A csúcsokhoz a hozzá tartozó lapokon szereplő számok összegét írtuk. Határozd meg a lapok összes lehetséges megszámozását úgy, hogy a csúcsokhoz írt számok egyformák legyenek. Azt tudjuk, hogy két szomszédos lapon a 4-es és a 9-es szám található. A szomszédos lapoknak közös az élük.
-
Egy négyzet csúcsaiba az 1, 2, 3, 4 számokat írtuk. Palkó mindig a négyzet három szomszédos csúcsában változtathatja meg a számokat, a következőképpen: vagy mind a hármat 1-gyel megnöveli, vagy mind a hármat l-gyel csökkenti (ábra). Elérheti-e ezzel a módszerrel azt, hogy a négyzet minden csúcsában 4-es
legyen?
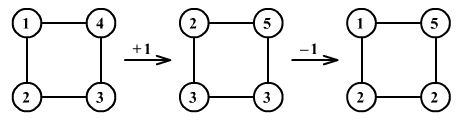
Az alábbi ábrán szemléltetett esetek közül melyeket tudja Palkó a fent leírt módszerrel megvalósítani? (Miért?)
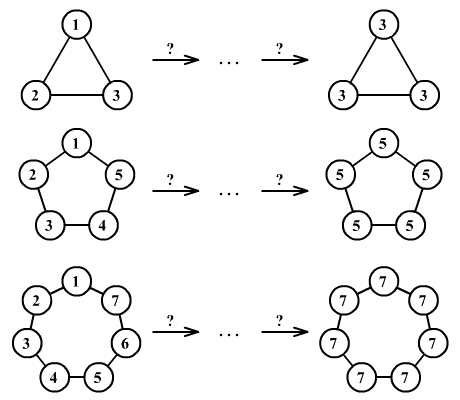
|
