Nagyszabadiban polgármestert választottak. A község három szavazókörzetében a polgárok két jelöltre szavazhattak: Buzgó mérnökre és Lelkes doktornőre. Az első két szavazókörzetben a leadott voksok alapján 7:5, illetve 5:3 arányban Lelkes doktornő győzött, a harmadikban 3:7 arányban Buzgó mérnök bizonyult jobbnak. A választás végül döntetlent hozott, mivel mind a két jelölt ugyanannyi szavazatot kapott. Határozzuk meg az egyes szavazókörzetekben leadott érvényes szavazatok számának arányát, ha tudjuk, hogy az első két körzetben az érvényes szavazatok száma azonos volt!

Az ABCD egyenlőszárú trapéz (hosszabbik alapja AB) A csúcsán keresztül két egyenes húzható, amelyek a trapézt három egyenlőszárú háromszögre osztják. Mekkorák a trapéz szögei?

Határozd meg mindazon természetes (x, y) számpárokat, amelyekre teljesül az alábbi egyenlet:
1 + x + y + xy = 2008

Az ábrán látható  ABCD  négyzet oldala  a,  a  KLMN  téglalap oldalai  KL = 3a  és  LM = a.  Az  ABCD  négyzetet forgassuk el  B  csúcsa körül az óramutató járásával megegyező irányba úgy, hogy az elforgatott  BC  oldal az  MN  oldalra illeszkedjen. A négyzetet addig forgatjuk csúcsai körül (lásd ábra), amíg az a téglalap kerülete mentén haladva újból vissza nem tér kiinduló helyzetébe.

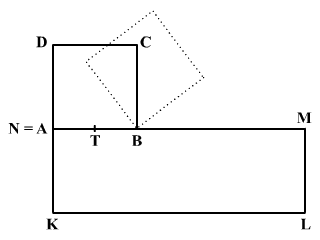
a) Szerkeszd meg az  AB  oldal  T  felezőpontjának pályáját, amelyen a mozgás során végighalad!
b) Számítsd ki a  T  pont által leírt zárt görbével határolt síktartomány területét!