Keresd meg az összes olyan 9-re végződő négyjegyű számot, amely összes számjegyével osztható!

Peti azt tudakolta nagymamájától, hány éves lehet a nagyapó. A nagyi így felelt: „Régen túl vagyunk már az ötvenen, de még nem töltöttük be a nyolcvanat. Ha nagyapád és az én életkorom összegét megszorzod azok különbségével és az eredményhez hozzáadod mindkettőnk életkorát, akkor 492-t kapsz .” Hány éves nagyapó, ha tudjuk, hogy nagymamánál idősebb?

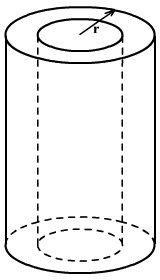
Egy m magasságú, r sugarú forgáshengerbe, annak tengelyét követve henger alakú lyukat fúrtunk. Az így létrejött „üreges henger” térfogata az eredeti henger térfogatának fele. Fejezd ki az „üreges henger” falának vastagságát r segítségével!

A tavalyi színházi évadban a belépőjegyek egységes ára 160 Sk volt. Idén az ülőhelyeket két kategóriába sorolták. Az I. kategóriába sorolt helyek ára 180 Sk, a II. kategóriába soroltaké 155 Sk. Ha az összes jegy elkel, a bevétel így ugyanakkora lesz, mint amilyen a tavalyi szezonban volt teltháznál. A színházigazgató elégedetlen és a jövi szezonra változást tervez: a II. kategória legrosszabb helyeit III. kategóriába sorolja át. Hogy a bevétel teltháznál ne változzon, úgy döntött, hogy a belépőjegyek ára 180 Sk (I. kategória), 160 Sk (II. kategória) és 130 Sk (III. kategória) lesz. Milyen arányban lesznek elosztva az ülőhelyek kategóriák szerint a jövi évadban?

Gyuri két csokit vásárolt az iskola előtti boltban. Misi ugyanilyen két csokoládét vásárolt az iskola mögötti boltban, és Pisti is vett egy ilyen csokit az iskolai büfében. Kiszámolták, hogy ha mindhárman az iskola előtti boltban vásároltak volna, akkor összesen 6 koronát takarítottak volna meg, ha pedig az iskola mögötti boltban vásárolnak, akkor összesen 6,50 koronával fizettek volna többet. Az iskolai büfében egy csoki 19,50 Sk-ba kerül. Mennyibe került összesen az öt csokoládé? Mennyibe kerül a csokoládé az iskola mögötti boltban?

Adott a síkban egy ABCD négyszög. Szerkeszd meg a K és L pontokat úgy, hogy BCDK és CDAL paralelogrammák legyenek. Igazold, hogy az AB szakasz felezőpontja a KL egyenesre esik!