-
Az első tényező ötször
nagyobb, mint a második tényező. Írd le az első és a második tényező
hányadosát!
-
Melyik szám következik a
122 után a számsorozatban?
1, 2, 5, 14, 41, 122, ...
-
Írd le a 2006
legnagyobb osztóját!
-
Melyik számmal kell
megszorozni a 12 345 679-et,
hogy a szorzat 333 333 333 legyen?
-
Melyik törzsalakú törttel
kell helyettesíteni a
 -t
a feladatban:
-t
a feladatban:
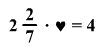
-
Hány nulla lesz a szorzat
eredményében?
(2030 – 30).(2400 – 400).(1980 + 20).(1650 + 350) =
-
Írd le, hogy milyen
számjegyre végződik a szorzat:
20,274 . 21,306 =
-
Számítsd ki:
508 . 1003 – 2006 . 254 =
-
Egy 30
cm magas hatliteres edényben 4,5 l víz van. Hány
deciméter magasságig ér a víz?
-
Hány 30-nál kisebb kétjegyű
prímszám van?
-
Hány centiméter hosszú az 50 cm2
területű egyenlőszárú derékszögű háromszög befogója?
-
Számítsd ki:
3,4 – ( 1,4 – ( 7,4 – 10,4 ) ) ) =
-
Három és egy negyed kenyér
78 koronába kerül. Hány koronába kerül kettő és fél ilyen kenyér?
-
Írd le az eredményt:
–10,25 : (–0,2) : 2000 : (–5) : 0,05 : 0,02 =
-
A számegyenesen az
5 és a 15 egymástól 2 dm
távolságra vannak. Hány centiméter távolságra lesznek egymástól a
–5 és a –7 számok?
