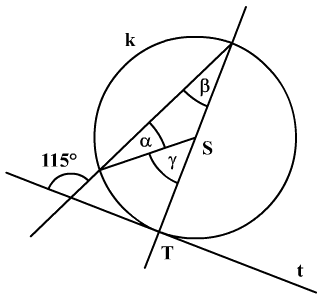
Határozzátok meg az ábrán látható  α,  β,  γ  szögek összegét, ha a  t  a  k(S,r)  körvonalhoz húzott érintő,  T  pedig az érintési pont.

Számítsd ki és az eredményt írd le:

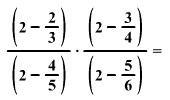
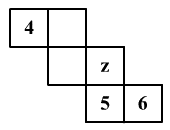
A dobókockán a számok úgy helyezkednek el, hogy a szemközti lapokon levő számok összege mindig 7. Milyen szám rejtőzik a z-vel jelölt lapon?

Jelekből sorozatot alkottunk:

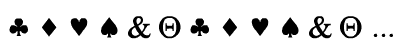
Milyen jel van a 81. helyen?

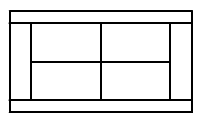
Hány téglalap van a teniszpályán?

Az ABCDEFGH kockában számítsd ki a leghosszabb AG szakasz hosszának négyzetét, ha az A, B pontok távolsága .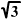

Hány olyan  XXZZYKKL  alakú nyolcjegyű szám van, amely a 0, 2, 4, 5, 8 számjegyeket tartalmazza, a K kétszerese az X -nek, és minden betű más számjegyet jelöl.

Számítsd ki és az eredményt írd le tizedestört alakban!

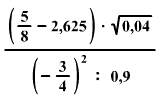
Számítsd ki és írd le mindhárom eredmény összegét!

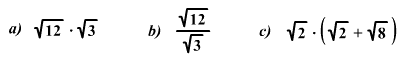
Hány másodperc az 1 óra 15 %-a?

Számítsd ki:
2,203 + 2,209 + 2,211 + 2,215 + 2,219 – 2,205 – 2,207 – 2,213 – 2,217 =

Oldd meg az egyenletet:
x² – 2x + 1 – 2 = ( x + 1 )² – 3x

Az ábrán látható ABC háromszög AB oldalán levő K és L pont egyforma részekre osztja az oldalt. A CK szakaszon az M, N pontok szintén egyforma részekre osztják a szakaszt. Számítsd ki az ABC háromszög területét, ha az MNB háromszög területe 3,4 cm².

Számítsd ki az 1000 cm³ térfogatú kocka felszínét!

A  2, 3, 5, 7, 8  számokat tartalmazó kártyákból rakd ki az összes olyan számot, amely számjegyeinek összege 20. Hány ilyen szám van?