Nissan Almera autó fogyasztása 6,7 liter 100 kilométeren. A Hyundai Akcent autó fogyasztása 108 milliliter 1 500 méteren. Az Almera vagy az Akcent fogyaszt többet 100 kilométeren?

Nyáron napközben egy óra internethozzáférés díja 5,4 €-ba került. Ősszel a hozzáférés az ár egy kilencedével csökkent, a karácsony utáni akcióban pedig még csökkentették az új ár egy hatodával. Hány €-ba került a hozzáférés a két árcsökkentés után?

Írd le azt a számot, amelyik nem tartozik a többi közé:
7612, 2354, 4312, 3654, 6754

Az osztályban 12 lány és 16 fiú van. Az átlagmagasságuk 165 cm. Hány centiméter magasak összesen?

Írjátok le azt a számot, amelyik az egyenlet gyöke:

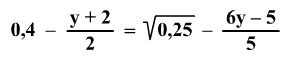
A DAC bajnoki mérkőzéseire, ha otthon játszanak, a nők és a gyerekek ingyen mehetnek be. A férfiaknak a jegy 8 €-ba kerül. A férfiak, nők és gyerekek aránya 15 : 3 : 2. A jegyekért összesen 12 000 €-t szedtek be. Írjátok le, hogy összesen hány néző volt a lelátón!

Számítsd ki és írd le az eredményt:
27 . 61 + 27 . (–60) + 27 . 62 + 27 . (–59) + 27 . 63 + 27 . (–58) – 3 . 81 =

A 6 cm alapú trapézt az átlója egy 10 cm² és egy 12 cm² területű háromszögre osztja. Számítsd ki a másik alap hosszát centiméterekben!

Milyen számjegyre végződik a kivonás eredménye:
2009²⁰⁰⁹ – 7

Írd le azt a betűt, amelyik a legkisebb számot jelöli:
A: 0,9²     B: 0,09³     C: 0,009²     D: 0,125²     E: 0,0009²

A téglalap háromszögekre van felosztva, amelyek területei cm²-ben vannak feltüntetve. Hány négyzetcentiméter a jelöletlen háromszög területe?

Számítsátok ki:
12,5 : 0,25 : 0,2 : 0,5 : 0,2 =

Ha leírunk egy tetszés szerinti kétjegyű számot és a számjegyeit összeadjuk, hány különböző összeget kaphatunk?

Milyen számjegyre végződik a szorzat:
12 . 134. 145 . 146 . 157 . 269 . 2009 =

Az óra 10⁰⁰ órát mutat. Írd le annak a tompaszögnek a nagyságát, amelyet az óramutatók 15 perc múlva fognak bezárni!