A villamosok a közös végállomásra a következőképpen érkeznek: a 7-es villamos 45 percenként, a 11-es 1,5 óránként és a 9-es 50 percenként. Reggel 6:00 órakor egyszerre indulnak ki az útjukra. Legközelebb hány óra múlva találkozik az összes villamos a végállomáson?

Zsófi leírta a  456745674567...  számot, amelynek 102 számjegye volt. Írjátok le ennek a számnak a számjegyeinek az összegét!

Máté zsebében nyolc tízkoronás, öt kétkoronás és tíz ötkoronás van. Legkevesebb hányszor kellett a zsebébe nyúlnia ahhoz, hogy biztosan kihúzzon egy ötkoronást? Minden alkalommal csak egy érmét húz ki.

Számítsátok ki:

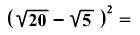
Réka rendet rakott a polcon a cédéi között. A jobb áttekintés végett megszámozta a cédéket. Hány cédéje volt Rékának, ha a pontosan középen levő cédén a 11-es szám volt?

Az egyenlet megoldását írjátok fel törzsalakú tört alakjában!

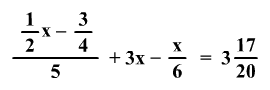
Hányszorosára növekszik a téglatest térfogata, ha minden élét a háromszorosára növeljük?

Számítsátok ki az ABCDEFGH kocka élét, ha az ACGE négyszög területe 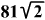 dm².

A 8.A osztályban az első félévben megfelelt a 18 fiúból 16 és az összes lány. Az összes tanuló 5%-a nem felelt meg. Írjátok le, hogy hány tanuló járt a 8.A osztályba?

A dobozban kártyák voltak, amelyeken egy szám összes osztói voltak. Laci megállapította, hogy az ott található számok közül a 72 a legnagyobb. Melyik szám osztói voltak?

Számítsátok ki:
15 632² – 15 630² =

2007.1.1-jén 10 000 Sk-t tettem a betétkönyvre. Egy év múlva 300 Sk kamatot kellett volna hozzáírniuk. A banknak ezt az összeget először meg kell adóztatnia, ezért csak 243 Sk-t írtak hozzá. Hány százalékos kamatra van a pénzem elhelyezve a bankban?

Az összeadás eredményét írjátok le törzsalakú tört alakjában:

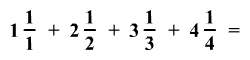
Mekkora szöget ír le az óra kismutatója az idő alatt, amely alatt a nagymutató 840°-os szöget ír le?

Milyen számjegyre végződik az eredmény:
2008²⁰⁰⁸ – 16 =