Hány hatjegyű szám jegyeinek szorzata 750?

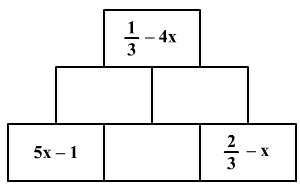
A számpiramis minden mezőjében az alatta levő két mezőbe írt szám összege szerepel (a legalsó sor mezőiben szereplő számokat kivéve). Írd be a megfelelő kifejezéseket az ábrán látható számpiramis üres mezőibe!

Egy 2 cm sugarú körbe írt ABCDEF hatszögben az FE és CD egyenesek metszéspontja M. Számítsd ki az AM szakasz hosszát!

Egy matematikai versenyen 142 tanuló vett részt. A verseny végén az egyik szervező észre vette, hogy a harmadik feladatért az egy főre jutó átlagos pontszám 2,7 (tizedekre kerekítve). Mivel a harmadik feladatot nem adta le az összes versenyző, ezért a leadott harmadik feladatra jutó átlagos pontszám 3,9 (tizedekre kerekítve) volt. Hány versenyző adta le a harmadik feladatot? (Megjegyzés: A feladatokra csak egész pontok jártak, a le nem adott feladat 0 pontot ért.)

Az REZ háromszöget, melynek területe  300 cm²,  |RE| = 25 cm  és  |ZE| = 30 cm,  két egyenes vágással három részre osztottunk és a darabokból (egymást nem fedve) téglalapot állítottunk össze. Határozd meg a téglalap oldalhosszait! Találd meg az összes lehetőséget!

Igazold, hogy az  (1.3.5.7. ... .2003.2005) + (2.4.6.8. ... .2004.2006)  szám osztható  2007⁴-nel!