|
|
|
Matematikai Olimpia, 9. évf., 2005/06, I. ford. feladatai
-
Határozzátok meg azon
háromjegyű természetes számok számát, amelyeknek pontosan két egyforma
számjegyük van.
-
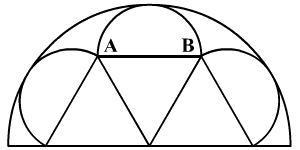
Az ábrán három egyenlőoldalú
háromszög, egy 1 dm sugarú nagy félkör és három kis félkör látható.
Határozzátok meg az AB szakasz hosszát.
-
A koordinátarendszerben adva
van három pont A[3,2], B[-1,1], C[-2,4] és ezen pontok
origó szerinti szimetrikus képei A', B', C'.
Határozzátok meg az ABCA'B'C' hatszög területét.
-
Az öreg vállalkozó meghalt és
hátrahagyott két számlát, egy pénzadóssági számlát és egy végrendeletet. A
végrendeletben az állt, hogy az első számlán lévő pénzt az 1. és 2. fia
között osszák szét 1:2 arányban, a második számlán lévő pénzt az 1. és 3.
fia között 1:3 arányban és az adósságot a 2. és 3. fia fizesse ki 2:3
arányban. Határozzátok meg, hogy hány korona volt az egyes számlákon és
milyen volt az adósság nagysága, amelyet a fiúknak kellet kifizetni, ha
tudjátok, hogy a végén mindegyikük 123456 koronát kapott.
-
Adva van két egyenlőoldalú
papírháromszög, a kisebbik területe 60 cm2. Ezen háromszögeket
úgy helyeztük egymásra, hogy a közös részük 30 cm2 területű
derékszögű háromszöget alkot. Mennyi lehetett a nagyobbik egyenlőoldalú
háromszög legkisebb területe?
-
Az írásbeli feladat 26 kérdést
tartalmazott, amelyek nehézségük szerint három csoportra voltak osztva. Az
első csoportban a helyes válasz három pontot ért, a másodikban ötöt a
harmadikban nyolcat. Maximálisan 111 pontot lehetett szerezni. Hány kérdés
lehetett az egyes csoportokban?
|
