Gyuri építőkészletében 64 egyforma nagy kocka van. A kockák oldallapjai egyszínűek - feketék vagy fehérek. Az összes kockából összerakható egy nagy kocka, amelynek minden egyes oldallapja fele-fele arányban fekete ill. fehér. Legfeljebb hány teljesen fehér kocka lehet Gyuri építőkészletében? Készítsetek ábrát arról, hogyan látjuk a nagy kockát alulról, hátulról, elölről, fentről, balról és jobbról nézve!

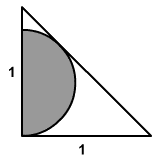
Határozzátok meg a derékszögű egyenlő szárú háromszögbe írt félkör területét (lásd az ábrát)! Az ábrán a számadatok decimétert jelentenek.

Írjátok fel háromféleképpen a 2004-et néhány egymás után következő természetes szám összegeként!

Ha egy példában, amely két természetes szám összeszorzására vonatkozik, az első tényezőt tízesekre kerekítjük, a szorzat 48-cal megnövekszik. Ha az eredeti példában a második tényezőt kerekítjük tízesekre, az eredeti szorzat 1512-vel csökken. Keressük meg az eredeti példát (írjuk fel az összes lehetőséget)!

Dóra, Mari, Józsi és Peti méredzkednek. A legnehezebb és a legkönnyebb közülük együtt 113 kg. Dóra, Mari és Józsi együtt 169 kg, Mari, Józsi és Peti együtt 166 kg, Dóra és Peti együtt összesen 99 kg. Milyen nehezek a gyerekek külön-külön, ha tudjuk, hogy közöttük nem Józsi a legnehezebb?

Keressük meg azokat az  a, b  természetes számokat, amelyekre érvényesek a következő feltételek:
  •  3a + b = 165 ,
  •  az  a, b  számok legkisebb közös többszöröse tízszer nagyobb ugyanezen  a, b  számok legnagyobb közös osztójánál.