|
|
|
Matematikai Olimpia, 9. évf., 2002/03, I. ford. feladatai
-
Írjatok a 683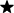 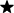 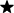 számban a csillagok helyére megfelelő számjegyeket úgy, hogy ez a hatjegyű szám osztható legyen
7-tel, 8-cal és 9-cel! számban a csillagok helyére megfelelő számjegyeket úgy, hogy ez a hatjegyű szám osztható legyen
7-tel, 8-cal és 9-cel!
-
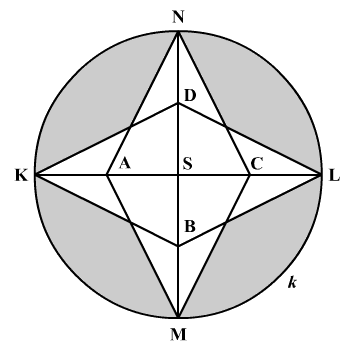
Számítsátok ki az ábrán látható, szürkével kijelölt rész területét, ha tudjuk, hogy a KL és MN szakaszok a k(S;6cm) kör egymásra merőleges átmérői, az A, B, C és D pontok pedig rendre a KS, MS, LS és NS szakaszok középpontjai!
-
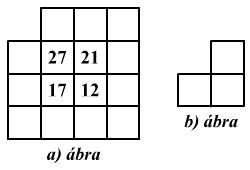
Az a) ábrán látható táblázatba úgy írták be a számokat, hogy a táblázat valamennyi, három négyzetből álló,
b) ábra szerinti alakzatainak bármelyikében a beírt három szám összege egyenlő. A három négyzetből álló alakzat nem fordítható el! Számítsátok ki a táblázatba beírt összes szám összegét!
-
Az l(A;r1) és
m(B;r2) körök középpontjai a k(S;r) kör átmérőjén
helyezkednek el. Az l és m körök kívülről érintik egymást és mindkettő érinti a k kört is. Rajtuk kívül a k körben fekszik az kör is, amely mindhárom kört (tehát az l, m és k köröket) érinti. Sárika azt gondolja, hogy az ACS háromszög kerülete nagyobb, mint a k kör átmérője. Igaza van? Miért?
-
Egy iskolában a diákok átlagéletkora 10 év, a pedagógusoké 54 év, az összes diák és pedagógus átlagéletkora együtt 12 év. Állapítsátok meg, hogy ebben az iskolában átlagosan hány gyerek van egy osztályban, ha tudjuk, hogy a pedagógusok átlagosan 21 órát tanítanak hetente, és a diákoknak hetente átlagosan 24 órájuk van!
-
Misi általában gyalog jár haza az iskolából. Ha kerékpárral megy haza, átlagsebessége 10 km/ó-val növekszik, és 15 perccel hamarabb ér haza. Ha édesapja autóval viszi haza, a gyalogláshoz viszonyítva átlagsebessége a hatszorosára nő, és 20 perccel hamarabb ér haza.
Milyen messze lakik Misi az iskolától? (Gyalog, kerékpárral, autóval is mindig ugyanazon az útvonalon halad.)
|
