Az ábrán egy "majdnemmágikus" zsebkendő látható. A zsebkendő fehér-fekete színű, ahol a fekete részek négyzetek, a fehér részek téglalapok. Ha a fehér és fekete részeknek egyenlő lenne a területe, akkor a zsebkendő mágikus lenne. 

Milyen méretei vannak annak a mágikus zsebkendőnek, amelyre igaz, hogy
  a)  középső négyzetének területe 324 cm²?
  b)  sarkainál levő négyzetek területe 16 cm²?

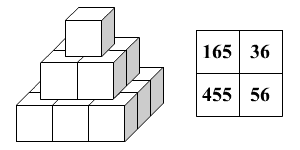
Az ábrán látható piramis természetes számokkal megszámozott kockákból áll. Az alsó szinten semelyik két kockának nincs ugyanolyan számja. A többi szinten levő kockák száma egyenlő az alatta levő 4 kocka számjainak összegével. Határozzátok meg, hogy milyen számjai vannak a kockáknak az alsó és felső szinten, ha tudjátok, hogy a középső szinten levő kockák úgy vannak megszámozva, ahogy az alábbi ábra mutatja.

A tetraéder két élének hossza 2 cm és 6 cm. Határozzátok meg a tetraéder többi élének hosszát, ha tudjátok, hogy a tetraéder mindegyik lapjának kerülete egyenlő és a tetraéder hálózatának lehető legkisebb kerülete 18 cm.

Határozzátok meg, az a lehető legtöbb százalékot, amennyivel megváltozhat (az eredeti értékére nézve) a következő egyenlet gyöke:
a . x  =  b   (a≠0),  ahol x ismeretlen,
ha az egyenlet egyik együtthatóját sem változtatjuk meg több mint 20%-ával az eredeti értéknek.