Az  505 505-öt elosztjuk öttel. Hány egyes számjegy lesz a hányadosban?

Melyik számmal kell megszorozni a  12 345 679-et, ahhoz, hogy  444 444 444-et kapjunk?

Írjátok le a feladat eredményét törzsalakú tört alakjában:

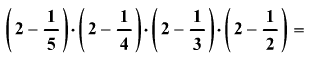
Írjátok le, hogy hány fok lesz a szabályos ötszög belső szögeinek az összege!

Írjátok le a héttel való osztás utáni összes lehetséges maradék szorzatát!

A derékszögű háromszögben az egyik hegyes szög nagysága 47° 54'. Írjátok le, hogy hány fok ebben a háromszögben a külső szögek összege!

Hányszorosára növekszik a kocka térfogata, ha az élét a háromszorosára növeljük?

Milyen számot kell az egyenletben az  x  helyére írni, hogy érvényes legyen:

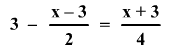
A  9 728 340  számban húzzatok át 2 számjegyet úgy, hogy a lehető legnagyobb 12-vel osztható számot kapjátok! Írjátok le az így kapott számot!

Számítsátok ki:
2001 + 2002 + 2003 + 2004 + 2005 + 2006 + 2007 + 2008 – 1901 – 1902 – 1903 – 1904 – 1905 – 1906 – 1907 – 1908 =

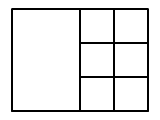
Írjátok le, hogy hány négyszög van az ábrán:

Írjátok le, hogy egy óra 20%-a hány másodperc!

Gergőnek 3 lánytestvére van és mindegyik lánytestvérének két fiútestvére van. Írjátok le, hogy hány gyerek van a családban!

Két egész számra gondoltam. Ha összeszoroztam a két számot, akkor  –12  lett az eredmény. Aztán összeadtam a két számot, akkor meg  1  lett az eredmény. Írjátok le a gondolt számok közül a nagyobbat!

Számítsátok ki a 144 összes pozitív osztója közül a legnagyobb és a legkisebb osztó szorzatát!