Írjátok le azt a számot, amely az egyenlet megoldása:

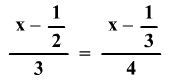
Az autó 5 000 €-ba kerül. A klímaberendezés beszerelése után 10%-kal drágult. Amikor a vevő meg akarta venni, észrevette, hogy az autó meg van karcolva, ezért felajánlottak neki 10%-os kedvezményt. Hány eurót fizetett a vevő ezért az autóért?

Milyen számjegyre végződik a  2007²⁰⁰⁷ ?

Számítsd ki:
0,125 : 0,25 : 0,2 : 0,5 : 0,2 : 0,5 =

Gondoltam két számra. Ha összeszorzom a számokat  –24-et, ha összeadom a számokat, akkor  5-öt kapok. Írd le a gondolt számok közül a nagyobbat!

A  123 456 789  számból húzz ki két számjegyet úgy, hogy a megmaradt szám a lehető legnagyobb hárommal osztható szám legyen. Írd le a megmaradt számot!

Melyik az a legnagyobb természetes szám, amelyet az  x  helyére írhatsz úgy, hogy érvényes legyen az egyenlőtlenség:

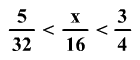
Máté megkérdezte az osztálytársától, hogy hányas a szekrénykéjének a száma. Az osztálytárs így felelt: "Az én szekrénykémnek a száma 14-gyel való osztás után 5-öt ad és a maradék 7". Írd le a szekrényke számát!

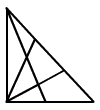
Hány háromszög van az ábrán?

Számítsd ki:
1 173 : 17 – 969 : 17 + (100 + 30 + 6) : 17 =

A pénztárcámban csak ötkoronás és kétkoronás érmék vannak. Hányféleképpen tudok ezekkel az érmékkel kifizetni 150 Sk-t?

Gondoltam egy természetes számra. Ha elosztom héttel, akkor a maradék 3, ha néggyel osztom el, akkor a maradék 0. Írd le a legkisebb számot ezzel a tulajdonsággal!

Az  1 288-as szám prímtényezős felbontásában hányszor szerepel a 2-es szám?

Írd le azt a betűt, amely a legnagyobb számot rejti:
P = 0,2²
Y = 0,004
T = 0,2³
A = – 0,2²
G = – 0,0004
O = 0,15²
R = 0,0369³

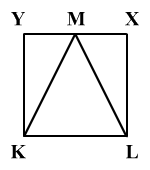
Hány négyzetcentiméter az ábrán látható KMY háromszög területe, ha KLXY négyzet oldalának a hossza 4,4 cm és az M pont felezi az XY oldalt?