-
Hány négyzetméter
a 22,9 m2 + 9600 mm2
+ 22,1 dm2 ?
-
A könyv oldalainak megszámozásához
1392 számjegyre volt szükség. Hány oldalas a könyv?
-
Az iskolában 6 osztály van.
Az elsőben, a másodikban és a harmadikban együtt 120 tanuló
van. A negyedik osztályban 8-cal kevesebb tanuló van mint a harmadik
osztályban, az ötödik osztályban 10-zel több tanuló van mint az
első osztályban, és a hatodik osztályban 2-vel több tanuló
van mint a második osztályban. Hány tanuló van az egész iskolában?
-
A nagy nyomtatott ábécé
melyik betűi középpontosan szimmetrikusak?
-
Számítsd
ki: 834 . 35 - 836 . 37
-
Az osztály tanulói kettesével
sétáltak. Az egyik tanuló maga elé nézett és 9 párt számolt
meg. Utána hátra fordult és itt 5 párt számolt meg. Hány tanuló
volt az osztályban?
-
Hat falu: A, B, C, D, E, F
egy szabályos hatszög csúcsait alkotják (lásd ábrát).
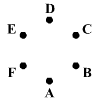
Három barát: Feri, Misi és Jancsi végigjárják mind a hat falut:
Jancsi a következő útvonalon ment:
B - D - A - C - F - E
Feri ezen az útvonalon:
B - D - F - A - C - E
Misi pedig ezen az útvonalon:
B - D - E - A - C - F
Ki ment a leghosszabb és ki a legrövidebb útvonalon?
-
Három egymás után következő
szám szorzata 120. Melyek ezek a számok?
-
A vasrúd 1 m hosszú. A rúd
szétvágása két részre 50 fillérbe kerül. Mennyibe kerül a rúd
szétvágása 10 egyforma részre?
-
Legtöbb hány részre lehet
szétosztani egy kört 4 egyenessel?
-
Számítsátok
ki: - 622 - [ - 435 - ( - 387 ) ] .
-
Számítsd ki az a =
0,28 m élű kocka felszínét. Fejezd ki ennek a kockának
a felszínét négyzetcentiméterekben.
-
A csillagok helyére írjatok
számtani műveleti jeleket úgy, hogy érvényes legyen:
5 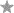 4
4 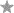 3
3
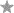 2 =
30
2 =
30
-
Hat pont: A, B, C, D,
E, F két olyan négyzet csúcsait alkotják, melyek élhossza
1. Hány olyan háromszög van, melyek területe 1/2 és a háromszög
csúcsai a kijelölt pontokban vannak?
-
A 431, 212, 125, 8
számok közül melyeket lehet behelyettesíteni az x helyébe
úgy, hogy a 2357 . x + 1432 - 511
kifejezés értéke páros legyen?
