Orsi, Előd, Zsuzsi és Tibi átlagmagassága 164 cm. Milyen magas Orsi, ha Előd, Zsuzsi és Tibi magasságának összege 506 cm .

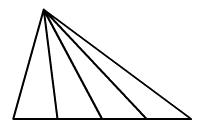
Hány háromszög van az ábrán?

Keressétek meg azt a két számot, amelyek összege 57 és egyik szám 60-nal nagyobb, mint a másik.

Hány olyan szám van, amely kisebb, mint  –1,4  és nagyobb, mint  –1,2 ?

Az S pont a BOKA négyzet középpontja. Mekkora az OSB nemkonvex szög nagysága?

Határozzátok meg az összes olyan háromjegyű természetes szám átlagát, amelyek mindhárom számjegye egyforma.

Legkevesebb hány derékszögű háromszögből tudjuk az árbán látható háromszöget kirakni úgy, hogy azok ne fedjék egymást?

Határozzátok meg az eredmény utolsó számjegyét:   636 . 363 – 636 : 6

Az egyenlőszárú háromszög oldalai 2 cm és 5 cm hosszúak. Mekkora az alap hossza?

Milyen számjegyekkel helyettesíthetjük a betűket az egyenlőségben?
L + O + S = L . O . S

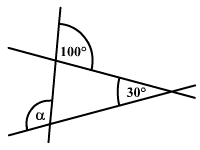
Számítsátok ki az ábrán látható α szög nagyságát!

Melyik szám 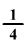-e éppen egy harmad?

Milyen számjegyre végződik a szorzat?
105 . ( 210 – 2 . 3 . 6 . 5 )

Számítsátok ki:
– 5 – ( – 3 – 6 ) – ( – 6 – 12 ) – ( + 22 )